
分析 直接利用偶函数的性质:在关于原点对称的区间上单调性相反即可得出其在(0,+∞)上的单调性;再利用函数单调性的定义证明结论即可.
解答 解:因为偶函数在关于原点对称的区间上单调性相反;
且f(x)在(-∞,0)上是增函数,
故f(x)在(0,+∞)是减函数.
证明如下:若0<x1<x2<+∞,那么-∞<-x2<-x1<0.
由于偶函数在(-∞,0)上是增函数,故有:f(-x2)<f(-x1)
又根据偶函数的性质可得:f(-x1)=f(x1),f(-x2)=f(x2)
综上可得:f(x1)>f(x2)
故f(x)在(0,+∞)上是减函数
点评 本题主要考查函数奇偶性与单调性的综合问题.这一类型题目,主要是考查偶函数在关于原点对称的区间上单调性相反,而奇函数在关于原点对称的区间上单调性相同这一结论.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2018 | B. | -2009 | C. | 2013 | D. | -2013 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
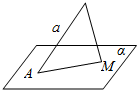 已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )
已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )| A. | 线段 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-1,0) | C. | (-1,1) | D. | (0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com