
【题目】已知椭圆![]() 的中心为原点
的中心为原点![]() ,焦点为
,焦点为![]() ,离心率为
,离心率为![]() ,不与坐标轴垂直的直线
,不与坐标轴垂直的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)若![]() 为线段
为线段![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
(2)若点![]() 是直线
是直线![]() 上一点,点
上一点,点![]() 在椭圆
在椭圆![]() 上,且满足
上,且满足![]() ,设直线
,设直线![]() 与直线
与直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,问
,问![]() 是否为定值?若是,请求出
是否为定值?若是,请求出![]() 的值;若不是,请说明理由.
的值;若不是,请说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,过抛物线![]() 上的一点
上的一点![]() 作抛物线的切线,分别交x轴于点D交y轴于点B,点Q在抛物线上,点E,F分别在线段AQ,BQ上,且满足
作抛物线的切线,分别交x轴于点D交y轴于点B,点Q在抛物线上,点E,F分别在线段AQ,BQ上,且满足![]() ,
,![]() ,线段QD与
,线段QD与![]() 交于点P.
交于点P.
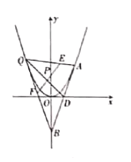
(1)当点P在抛物线C上,且![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在摩天轮底座中心![]() 与附近的景观内某点
与附近的景观内某点![]() 之间的距离
之间的距离![]() 为
为![]() m.摩天轮与景观之间有一建筑物,此建筑物由一个底面半径为
m.摩天轮与景观之间有一建筑物,此建筑物由一个底面半径为![]() m的圆柱体与一个半径为
m的圆柱体与一个半径为![]() m的半球体组成.圆柱的地面中心
m的半球体组成.圆柱的地面中心![]() 在线段
在线段![]() 上,且
上,且![]() 为
为![]() m.半球体球心
m.半球体球心![]() 到地面的距离
到地面的距离![]() 为
为![]() m.把摩天轮看做一个半径为
m.把摩天轮看做一个半径为![]() m的圆
m的圆![]() ,且圆
,且圆![]() 在平面
在平面![]() 内,点
内,点![]() 到地面的距离
到地面的距离![]() 为
为![]() m.把摩天轮均匀旋转一周需要
m.把摩天轮均匀旋转一周需要![]() min,若某游客乘坐摩天轮(把游客看作圆
min,若某游客乘坐摩天轮(把游客看作圆![]() 上的一点)旋转一周,求该游客能看到点
上的一点)旋转一周,求该游客能看到点![]() 的时长.(只考虑此建筑物对游客视线的遮挡)
的时长.(只考虑此建筑物对游客视线的遮挡)

查看答案和解析>>
科目:高中数学 来源: 题型:
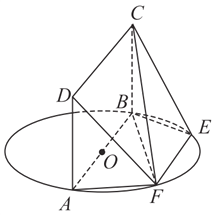
【题目】如图, ![]() 为圆
为圆![]() 的直径,点
的直径,点![]() ,
, ![]() 在圆
在圆![]() 上,
上, ![]() ,矩形
,矩形![]() 和圆
和圆![]() 所在的平面互相垂直,已知
所在的平面互相垂直,已知![]() ,
, ![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(Ⅲ)当![]() 的长为何值时,二面角
的长为何值时,二面角![]() 的大小为
的大小为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]()
![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,椭圆的上顶点为点
,椭圆的上顶点为点![]() ,点
,点![]() 为椭圆
为椭圆![]() 上一点,且
上一点,且![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若![]() ,过点
,过点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,求线段
两点,求线段![]() 的中点
的中点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
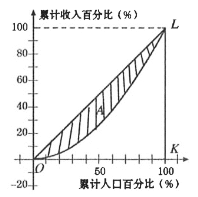
【题目】为了研究国民收入在国民之间的分配,避免贫富过分悬殊,美国统计学家劳伦茨提出了著名的劳伦茨曲线,如图所示:劳伦茨曲线为直线![]() 时,表示收入完全平等,劳伦茨曲线为折线
时,表示收入完全平等,劳伦茨曲线为折线![]() 时,表示收入完全不平等记区域
时,表示收入完全不平等记区域![]() 为不平等区域,
为不平等区域,![]() 表示其面积,
表示其面积,![]() 为
为![]() 的面积.将
的面积.将![]() ,称为基尼系数.对于下列说法:
,称为基尼系数.对于下列说法:
①![]() 越小,则国民分配越公平;
越小,则国民分配越公平;
②设劳伦茨曲线对应的函数为![]() ,则对
,则对![]() ,均有
,均有![]() ;
;
③若某国家某年的劳伦茨曲线近似为![]() ,则
,则![]() ;
;
④若某国家某年的劳伦茨曲线近似为![]() ,则
,则![]() .
.
其中不正确的是:( )
A.①④B.②③C.①③④D.①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com