
| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{2}}{3}$ |
分析 根据线面角的定义先确定直线B1C与平面AB1D1所成的角平面角,然后根据条件进行求值即可.
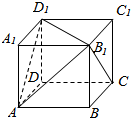
解答  解:以D为坐标原点,建立空间坐标系如图:
解:以D为坐标原点,建立空间坐标系如图:
则A(1,0,0),D1(0,0,1),B1(1,1,1),C(0,1,0).
则$\overrightarrow{{B}_{1}C}$=(-1,0,-1),$\overrightarrow{{AD}_{1}}$=(-1,0,1),$\overrightarrow{{AB}_{1}}$=(0,1,1),
设平面AB1D1的法向量为$\overrightarrow{n}$=(x,y,z),
则由$\left\{\begin{array}{l}\overrightarrow{n}•\overrightarrow{{AD}_{1}}=0\\ \overrightarrow{n}•\overrightarrow{{AB}_{1}}=0\end{array}\right.$,得$\left\{\begin{array}{l}-x+z=0\\ y+z=0\end{array}\right.$,令z=1,则x=1,y=-1,即$\overrightarrow{n}$=(1,-1,1).
则$\overrightarrow{n}$•$\overrightarrow{{B}_{1}C}$=(1,-1,1)•(-1,0,-1)=-1-1=-2,|$\overrightarrow{n}$|=$\sqrt{3}$,|$\overrightarrow{{B}_{1}C}$|=$\sqrt{2}$.
所以设直线B1C与平面AB1D1所成的角是θ,则sinθ=|cos($\frac{π}{2}$-θ)|=|$\frac{\overrightarrow{n}•\overrightarrow{{B}_{1}C}}{\left|\overrightarrow{n}\right|\left|\overrightarrow{{B}_{1}C}\right|}$|=|$\frac{-2}{\sqrt{3}×\sqrt{2}}$|=$\frac{\sqrt{6}}{3}$,
故选:C.
点评 本题只有考查空间直线和平面所成角的求法,利用向量法是解决空间角的基本方法,考查学生的运算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | -6 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com