(4,+∞)
分析:先作出F关于BC的对称点P,再作P关于AC的对称点M,因为光线从F点出发射到BC上的D点经BC反射后,入射光线和反射光线都经过F关于直线BC的对称点P点,又因为再经AC反射,反射光线经过P关于直线AC的对称点,所以只需连接MA、ME交AC与点N,连接PN、PA分别交BC为点G、H,则G,H之间即为点D 的变动范围.再求出直线FG,FH的斜率即可.
解答:∵A(-2,0),B(2,0),C(0,2),∴直线BC方程为x+y-2=0,直线AC方程为x-y+2=0
如图,
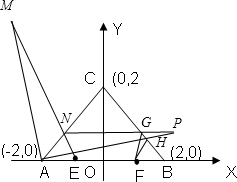
作F关于BC的对称点P,∵F(1,0),∴P(2,1),再作P关于AC的对称点M,则M(-1,4),
连接MA、ME交AC与点N,则直线ME方程为x=-1,∴N(-1,1)
连接PN、PA分别交BC为点G、H,
则直线PN方程为y=1,直线PA方程为x-4y+2=0,
∴G(1,1),H(

,

)连接GF,HF,
则G,H之间即为点D 的变动范围.
∵直线FG方程为x=1,直线FH的斜率为
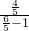
=4
∴FD斜率的范围为(4,+∞)
故答案为:(4,+∞).
点评:本题主要考查入射光线与反射光线之间的关系,入射光线与反射光线都经过物体所成的像,据此就可找到入射点的范围.

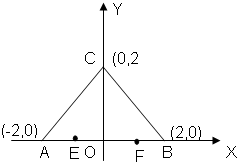 已知:A(-2,0),B(2,0),C(0,2),E(-1,0),F(1,0),一束光线从F点出发射到BC上的D点经BC反射后,再经AC反射,落到线段AE上(不含端点)FD斜率的范围为________.
已知:A(-2,0),B(2,0),C(0,2),E(-1,0),F(1,0),一束光线从F点出发射到BC上的D点经BC反射后,再经AC反射,落到线段AE上(不含端点)FD斜率的范围为________. 作F关于BC的对称点P,∵F(1,0),∴P(2,1),再作P关于AC的对称点M,则M(-1,4),
作F关于BC的对称点P,∵F(1,0),∴P(2,1),再作P关于AC的对称点M,则M(-1,4), ,
, )连接GF,HF,
)连接GF,HF,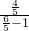 =4
=4

 已知点A(2,0),点M为曲线y=
已知点A(2,0),点M为曲线y= 如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.
如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.