
分析 令 2x=t>0,可得y=${(t-\frac{1}{2})}^{2}$+$\frac{3}{4}$,可得当t∈(0,$\frac{1}{2}$],即x∈(-∞,-1]时,函数y单调递减,从而得出结论.
解答 解:令 2x=t>0,可得y=t2-t+1=${(t-\frac{1}{2})}^{2}$+$\frac{3}{4}$,
故当t∈(0,$\frac{1}{2}$],即x∈(-∞,-1]时,函数y单调递减;
故当t∈($\frac{1}{2}$,+∞),即x∈(-1,+∞)时,函数y单调递增,
故函数y的减区间为∈(-∞,-1],
故答案为:(-∞,-1].
点评 本题主要考查复合函数的单调性、指数函数、二次函数的性质,属于中档题.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:选择题
| A. | [5,55] | B. | [5,50] | C. | [10,50] | D. | [10,55] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
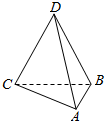 已知如图所示的三棱锥D-ABC的四个顶点均在球O的球面上,△ABC和△DBC所在平面相互垂直,AB=3,AC=$\sqrt{3}$,BC=CD=BD=2$\sqrt{3}$,则球O的表面积为( )
已知如图所示的三棱锥D-ABC的四个顶点均在球O的球面上,△ABC和△DBC所在平面相互垂直,AB=3,AC=$\sqrt{3}$,BC=CD=BD=2$\sqrt{3}$,则球O的表面积为( )| A. | 4π | B. | 12π | C. | 16π | D. | 36π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>-2 | B. | a≥-2 | C. | a>2 | D. | a≥2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
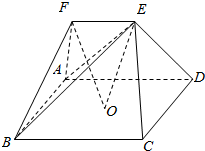 如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,△ABF是等边三角形,棱EF∥BC,且EF=$\frac{1}{2}$BC.
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,△ABF是等边三角形,棱EF∥BC,且EF=$\frac{1}{2}$BC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com