
【题目】设a∈Z,已知定义在R上的函数f(x)=2x4+3x3﹣3x2﹣6x+a在区间(1,2)内有一个零点x0 , g(x)为f(x)的导函数.
(Ⅰ)求g(x)的单调区间;
(Ⅱ)设m∈[1,x0)∪(x0 , 2],函数h(x)=g(x)(m﹣x0)﹣f(m),求证:h(m)h(x0)<0;
(Ⅲ)求证:存在大于0的常数A,使得对于任意的正整数p,q,且 ![]() ∈[1,x0)∪(x0 , 2],满足|
∈[1,x0)∪(x0 , 2],满足| ![]() ﹣x0|≥
﹣x0|≥ ![]() .
.
【答案】(Ⅰ)解:由f(x)=2x4+3x3﹣3x2﹣6x+a,可得g(x)=f′(x)=8x3+9x2﹣6x﹣6,
进而可得g′(x)=24x2+18x﹣6.令g′(x)=0,解得x=﹣1,或x= ![]() .
.
当x变化时,g′(x),g(x)的变化情况如下表:
x | (﹣∞,﹣1) | (﹣1, | ( |
g′(x) | + | ﹣ | + |
g(x) | ↗ | ↘ | ↗ |
所以,g(x)的单调递增区间是(﹣∞,﹣1),( ![]() ,+∞),单调递减区间是(﹣1,
,+∞),单调递减区间是(﹣1, ![]() ).
).
(Ⅱ)证明:由h(x)=g(x)(m﹣x0)﹣f(m),得h(m)=g(m)(m﹣x0)﹣f(m),
h(x0)=g(x0)(m﹣x0)﹣f(m).
令函数H1(x)=g(x)(x﹣x0)﹣f(x),则H′1(x)=g′(x)(x﹣x0).
由(Ⅰ)知,当x∈[1,2]时,g′(x)>0,
故当x∈[1,x0)时,H′1(x)<0,H1(x)单调递减;
当x∈(x0 , 2]时,H′1(x)>0,H1(x)单调递增.
因此,当x∈[1,x0)∪(x0 , 2]时,H1(x)>H1(x0)=﹣f(x0)=0,可得H1(m)>0即h(m)>0,
令函数H2(x)=g(x0)(x﹣x0)﹣f(x),则H′2(x)=g′(x0)﹣g(x).由(Ⅰ)知,g(x)在[1,2]上单调递增,故当x∈[1,x0)时,H′2(x)>0,H2(x)单调递增;当x∈(x0 , 2]时,H′2(x)<0,H2(x)单调递减.因此,当x∈[1,x0)∪(x0 , 2]时,H2(x)>H2(x0)=0,可得得H2(m)<0即h(x0)<0,.
所以,h(m)h(x0)<0.
(Ⅲ)对于任意的正整数p,q,且 ![]() ,
,
令m= ![]() ,函数h(x)=g(x)(m﹣x0)﹣f(m).
,函数h(x)=g(x)(m﹣x0)﹣f(m).
由(Ⅱ)知,当m∈[1,x0)时,h(x)在区间(m,x0)内有零点;
当m∈(x0 , 2]时,h(x)在区间(x0 , m)内有零点.
所以h(x)在(1,2)内至少有一个零点,不妨设为x1 , 则h(x1)=g(x1)( ![]() ﹣x0)﹣f(
﹣x0)﹣f( ![]() )=0.
)=0.
由(Ⅰ)知g(x)在[1,2]上单调递增,故0<g(1)<g(x1)<g(2),
于是| ![]() ﹣x0|=
﹣x0|= ![]() ≥
≥ ![]() =
= ![]() .
.
因为当x∈[1,2]时,g(x)>0,故f(x)在[1,2]上单调递增,
所以f(x)在区间[1,2]上除x0外没有其他的零点,而 ![]() ≠x0 , 故f(
≠x0 , 故f( ![]() )≠0.
)≠0.
又因为p,q,a均为整数,所以|2p4+3p3q﹣3p2q2﹣6pq3+aq4|是正整数,
从而|2p4+3p3q﹣3p2q2﹣6pq3+aq4|≥1.
所以| ![]() ﹣x0|≥
﹣x0|≥ ![]() .所以,只要取A=g(2),就有|
.所以,只要取A=g(2),就有| ![]() ﹣x0|≥
﹣x0|≥ ![]() .
.
【解析】(Ⅰ)求出函数的导函数g(x)=f′(x)=8x3+9x2﹣6x﹣6,求出极值点,通过列表判断函数的单调性求出单调区间即可.
(Ⅱ)由h(x)=g(x)(m﹣x0)﹣f(m),推出h(m)=g(m)(m﹣x0)﹣f(m),
令函数H1(x)=g(x)(x﹣x0)﹣f(x),求出导函数H′1(x)利用(Ⅰ)知,推出h(m)h(x0)<0.
(Ⅲ)对于任意的正整数p,q,且 ![]() ,令m=
,令m= ![]() ,函数h(x)=g(x)(m﹣x0)﹣f(m).
,函数h(x)=g(x)(m﹣x0)﹣f(m).
由(Ⅱ)知,当m∈[1,x0)时,当m∈(x0 , 2]时,通过h(x)的零点.转化推出| ![]() ﹣x0|=
﹣x0|= ![]() ≥
≥ ![]() =
= ![]() .推出|2p4+3p3q﹣3p2q2﹣6pq3+aq4|≥1.然后推出结果.
.推出|2p4+3p3q﹣3p2q2﹣6pq3+aq4|≥1.然后推出结果.
【考点精析】掌握利用导数研究函数的单调性和函数的极值与导数是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】为了解某社区居民有无收看“奥运会开幕式”,某记者分别从某社区60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,x人中,采用分层抽样的方法共抽查了30人进行调查,若在60~70岁这个年龄段中抽查了8人,那么x为( ) .
A. 90 B. 120 C. 180 D. 200
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)在R上为增函数,且f(1)= ![]() ,若实数a满足f(loga3)﹣f(loga
,若实数a满足f(loga3)﹣f(loga ![]() )≤1,则实数a的取值范围为( )
)≤1,则实数a的取值范围为( )
A.0<a≤ ![]()
B.a≤ ![]()
C.![]() ≤a<1
≤a<1
D.a≥3或0<a<1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心在
的圆心在![]() 轴上,并且过
轴上,并且过![]() 两点.
两点.
(1)求圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,那么以
两点,那么以![]() 为直径的圆能否经过原点,若能,请求出直线
为直径的圆能否经过原点,若能,请求出直线![]() 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为 ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)设X表示一辆车从甲地到乙地遇到红灯的个数,求随机变量X的分布列和数学期望;
(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,双曲线 ![]() =1(a>0,b>0)的右支与焦点为F的抛物线x2=2py(p>0)交于A,B两点,若|AF|+|BF|=4|OF|,则该双曲线的渐近线方程为 .
=1(a>0,b>0)的右支与焦点为F的抛物线x2=2py(p>0)交于A,B两点,若|AF|+|BF|=4|OF|,则该双曲线的渐近线方程为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
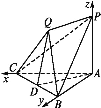
【题目】如图,在三棱锥P-ABC中,PA⊥底面ABC,△ABC是直角三角形,且PA=AB=AC.又平面QBC垂直于底面ABC.
(1)求证:PA∥平面QBC;
(2)若PQ⊥平面QBC,求锐二面角Q-PB-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,E,F分别是BB1,CD的中点.
(1)证明:平面AED⊥平面A1FD1;
(2)在AE上求一点M,使得A1M⊥平面DAE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px过点P(1,1).过点(0, ![]() )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.(14分)
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.(14分)
(1)求抛物线C的方程,并求其焦点坐标和准线方程;
(2)求证:A为线段BM的中点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com