
| A. | $\frac{5}{13}$ | B. | -$\frac{5}{13}$ | C. | $\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
科目:高中数学 来源: 题型:填空题
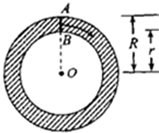 如图,我们知道圆环是线段AB绕圆心O旋转一周所形成的平面图形,所以,圆环的面积S=π(R2-r2)=(R-r)×2π×$\frac{R+r}{2}$可以看作是以线段AB=R-r为宽,以AB的中心绕圆心O旋转一周所形成的圆的周长2π×$\frac{R+r}{2}$为长的矩形面积.请将上述想法拓展到空间,并解决下列问题:若将平面区域M={(x,y)|(x-2)2+y2≤1}绕y轴旋转一周,则所形成的旋转体的体积是4π2.
如图,我们知道圆环是线段AB绕圆心O旋转一周所形成的平面图形,所以,圆环的面积S=π(R2-r2)=(R-r)×2π×$\frac{R+r}{2}$可以看作是以线段AB=R-r为宽,以AB的中心绕圆心O旋转一周所形成的圆的周长2π×$\frac{R+r}{2}$为长的矩形面积.请将上述想法拓展到空间,并解决下列问题:若将平面区域M={(x,y)|(x-2)2+y2≤1}绕y轴旋转一周,则所形成的旋转体的体积是4π2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 把正整数按一定的规律排成了如图所示的三角形数,设aij(i,j∈N+)是位于这个三角形数中从上往下数第i行,从左往右数第j列的数,如a32=5,若aij=2015,则i+j=( )
把正整数按一定的规律排成了如图所示的三角形数,设aij(i,j∈N+)是位于这个三角形数中从上往下数第i行,从左往右数第j列的数,如a32=5,若aij=2015,则i+j=( )| A. | 111 | B. | 110 | C. | 108 | D. | 105 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com