
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一.为坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村脱贫,坚持扶贫同扶智相结合,此帮扶单位考察了甲、乙两种不同的农产品加工生产方式,现对两种生产方式的产品质量进行对比,其质量按测试指标可划分为:指标在区间![]() 的为优等品;指标在区间
的为优等品;指标在区间![]() 的为合格品,现分别从甲、乙两种不同加工方式生产的农产品中,各自随机抽取100件作为样本进行检测,测试指标结果的频数分布表如下:
的为合格品,现分别从甲、乙两种不同加工方式生产的农产品中,各自随机抽取100件作为样本进行检测,测试指标结果的频数分布表如下:
甲种生产方式:
指标区间 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 | 30 | 15 | 15 |
乙种生产方式:
指标区间 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 | 30 | 20 | 10 |
(1)在用甲种方式生产的产品中,按合格品与优等品用分层抽样方式,随机抽出5件产品,①求这5件产品中,优等品和合格品各多少件;②再从这5件产品中,随机抽出2件,求这2件中恰有1件是优等品的概率;
(2)所加工生产的农产品,若是优等品每件可售55元,若是合格品每件可售25元.甲种生产方式每生产一件产品的成本为15元,乙种生产方式每生产一件产品的成本为20元.用样本估计总体比较在甲、乙两种不同生产方式下,该扶贫单位要选择哪种生产方式来帮助该扶贫村来脱贫?
【答案】(1)①优等品3件,合格品2件;②![]() ;(2)选择乙生产方式.
;(2)选择乙生产方式.
【解析】
(1)①根据频数分布表知:甲的优等品率为0.6,合格品率为0.4,即可得到抽去的件数;
②记3件优等品为![]() ,
,![]() ,
,![]() ,2件合格品分别为
,2件合格品分别为![]() ,
,![]() ,从中随机抽2件,列举出基本事件的总数,利用古典概型及其概率的计算公式,即可求解;
,从中随机抽2件,列举出基本事件的总数,利用古典概型及其概率的计算公式,即可求解;
(2)分别计算出甲、乙种生产方式每生产100件所获得的利润为![]() 元
元![]() 元,比较即可得到结论。
元,比较即可得到结论。
(1)①由频数分布表知:甲的优等品率为0.6,合格品率为0.4,所以抽出的5件产品中,优等品3件,合格品2件.
②记3件优等品为![]() ,
,![]() ,
,![]() ,2件合格品分别为
,2件合格品分别为![]() ,
,![]() ,从中随机抽2件,抽取方式有
,从中随机抽2件,抽取方式有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共10种,
共10种,
设“这2件中恰有1件是优等品的事件”为![]() ,则事件
,则事件![]() 发生的情况有6种,
发生的情况有6种,
所以![]() .
.
(2)根据样本知甲种生产方式生产100件农产品有60件优等品,40件合格品;乙种生产方式生产100件农产品有80件优等品,20件合格品.
设甲种生产方式每生产100件所获得的利润为![]() 元,
元,
乙种生产方式每生产100件所获得的利润为![]() 元,
元,
可得![]() (元),
(元),
![]() (元),
(元),
由于![]() ,所以用样本估计总体知乙种生产方式生产的农产品所获得的利润较高,该扶贫单位要选择乙生产方式来帮助该扶贫村来脱贫较好.
,所以用样本估计总体知乙种生产方式生产的农产品所获得的利润较高,该扶贫单位要选择乙生产方式来帮助该扶贫村来脱贫较好.


科目:高中数学 来源: 题型:
【题目】某公司为了解某产品的获利情况,将今年1至7月份的销售收入![]() (单位:万元)与纯利润
(单位:万元)与纯利润![]() (单位:万元)的数据进行整理后,得到如下表格:
(单位:万元)的数据进行整理后,得到如下表格:
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售收入 | 13 | 13.5 | 13.8 | 14 | 14.2 | 14.5 | 15 |
纯利润 | 3.2 | 3.8 | 4 | 4.2 | 4.5 | 5 | 5.5 |
该公司先从这7组数据中选取5组数据求纯利润![]() 关于销售收入
关于销售收入![]() 的线性回归方程,再用剩下的2组数据进行检验.假设选取的是2月至6月的数据.
的线性回归方程,再用剩下的2组数据进行检验.假设选取的是2月至6月的数据.
(1)求纯利润![]() 关于销售收入
关于销售收入![]() 的线性回归方程(精确到0.01);
的线性回归方程(精确到0.01);
(2)若由线性回归方程得到的估计数据与检验数据的误差均不超过0.1万元,则认为得到的线性回归方程是理想的.试问该公司所得线性回归方程是否理想?
参考公式:![]() ,
,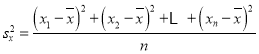 ,
,![]() ,
,![]() ;参考数据:
;参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面ABCD为正方形,![]() ,E,F分别是棱PC,AB的中点.
,E,F分别是棱PC,AB的中点.
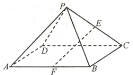
(1)求证:![]() 平面PAD;
平面PAD;
(2)若![]() ,求直线EF与平面PAB所成角的正弦值.
,求直线EF与平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某地区年龄在25~55岁的人员中,随机抽出100人,了解他们对今年两会的热点问题的看法,绘制出频率分布直方图如图所示,则下列说法正确的是( )

A. 抽出的100人中,年龄在40~45岁的人数大约为20
B. 抽出的100人中,年龄在35~45岁的人数大约为30
C. 抽出的100人中,年龄在40~50岁的人数大约为40
D. 抽出的100人中,年龄在35~50岁的人数大约为50
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的一个焦点为
的一个焦点为![]() ,点
,点![]() 在
在![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,问
两点,问![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形?若存在,求点
为直角顶点的等腰直角三角形?若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于方程为![]() 的曲线
的曲线![]() 给出以下三个命题:
给出以下三个命题:
(1)曲线![]() 关于原点对称;(2)曲线
关于原点对称;(2)曲线![]() 关于
关于![]() 轴对称,也关于
轴对称,也关于![]() 轴对称,且
轴对称,且![]() 轴和
轴和![]() 轴是曲线
轴是曲线![]() 仅有的两条对称轴;(3)若分别在第一、第二、第三、第四象限的点
仅有的两条对称轴;(3)若分别在第一、第二、第三、第四象限的点![]() ,都在曲线
,都在曲线![]() 上,则四边形
上,则四边形![]() 每一条边的边长都大于2;
每一条边的边长都大于2;
其中正确的命题是( )
A.(1)(2)B.(1)(3)C.(2)(3)D.(1)(2)(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形![]() 和矩形
和矩形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的中点.
的中点.
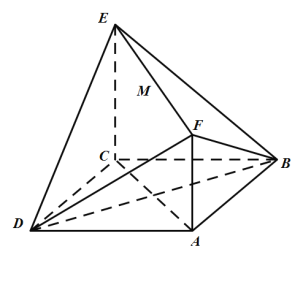
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的大小;
的大小;
(3)若线段![]() 上总存在一点
上总存在一点![]() ,使得
,使得![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按照国际乒联的规定,标准的乒乓球在直径符合条件下,重量为2.7克,其重量的误差在区间![]() 内就认为是合格产品,在正常情况下样本的重量误差
内就认为是合格产品,在正常情况下样本的重量误差![]() 服从正态分布.现从某厂生产的一批产品中随机抽取10件样本,其重量如下:
服从正态分布.现从某厂生产的一批产品中随机抽取10件样本,其重量如下:
2.72 2.68 2.7 2.75 2.66 2.7 2.6 2.69 2.7 2.8
(1)计算上述10件产品的误差的平均数![]() 及标准差
及标准差![]() ;
;
(2)①利用(1)中求的平均数![]() ,标准差
,标准差![]() ,估计这批产品的合格率能否达到
,估计这批产品的合格率能否达到![]() ;
;
②如果产品的误差服从正态分布![]() ,那么从这批产品中随机抽取10件产品,则有不合格产品的概率为多少.(附:若随机变量
,那么从这批产品中随机抽取10件产品,则有不合格产品的概率为多少.(附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.![]() 用0.6277,
用0.6277,![]() 用0.9743分别代替计算)
用0.9743分别代替计算)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com