
分析 (1)若a=3,求出A,B,即可求A∪B;
(2)若A∩B=A,A⊆B,分类讨论求实数a的取值范围.
解答 解:(1)将a=3代入A中不等式,得x2-2x-15<0,
解得-3<x<5,即A=(-3,5).
将a=3代入B中等式,得y=3x-6,
∵x≤2,∴0<3x≤9,即-6<3x-6≤3,
∴B=(-6,3],A∪B=(-6,5).
(2)∵A∩B=A,∴A⊆B,
由B中y的范围为-2a<y≤9-2a,即B=(-2a,9-2a).
由A看不等式变形,得x2-2x+1-a2-2a-1<0,
即(x-1)2-(a+1)2<0,整理得(x+a)(x-a-2)<0.
∵A∩B=A,∴A⊆B,
当a=-1时,A=∅,满足题意;
当a+2>-a,即a>-1时,A=(-a,a+2).
∵A⊆B,∴$\left\{\begin{array}{l}-2a≤-a\\ 9-2a≥a+2\end{array}\right.$
解得$0≤a≤\frac{7}{3}$; 当a+2<-a,即a>-1时,A=(a+2,-a).∴A⊆B,
∴$\left\{\begin{array}{l}-2a≤a+2\\-a≤9-2a\end{array}\right.$解得$-\frac{2}{3}≤a≤9$(舍去).
综上a=-1或$0≤a≤\frac{7}{3}$.
点评 本题考查集合的运算与关系,考查学生解不等式的能力,正确转化是关键.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:解答题
 已知以A(-1,2)点为圆心的圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
已知以A(-1,2)点为圆心的圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (8,1) | B. | (8,3) | C. | (-1,8) | D. | (7,8) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,7) | B. | (-1,6) | C. | (-1,7) | D. | (-2,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
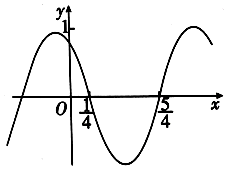
| A. | (kπ-$\frac{1}{4}$,kπ+$\frac{3}{4}$),k∈Z | B. | (2kπ-$\frac{1}{4}$,2kπ+$\frac{3}{4}$),k∈Z | ||
| C. | (k-$\frac{1}{4}$,k-$\frac{3}{4}$),k∈Z | D. | (2k-$\frac{1}{4}$,2k+$\frac{3}{4}$),k∈Z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com