
ЁОЬтФПЁПдВжмТЪЪЧдВЕФжмГЄгыжБОЖЕФБШжЕЃЌвЛАугУЯЃРАзжФИ![]() БэЪО.дчдкЙЋдЊ480ФъзѓгвЃЌФЯББГЏЪБЦкЕФЪ§бЇМвзцГхжЎОЭЕУГіОЋШЗЕНаЁЪ§ЕуКѓ7ЮЛЕФНсЙћЃЌЫћЪЧЪРНчЩЯЕквЛИіАбдВжмТЪЕФЪ§жЕМЦЫуЕНаЁЪ§ЕуКѓЕк7ЮЛЕФШЫЃЌетБШХЗжодчСЫдМ1000Фъ.ЩњЛюжаЃЌЮвУЧвВПЩвдЭЈЙ§ШчЯТЫцЛњФЃФтЪдбщРДЙРМЦ
БэЪО.дчдкЙЋдЊ480ФъзѓгвЃЌФЯББГЏЪБЦкЕФЪ§бЇМвзцГхжЎОЭЕУГіОЋШЗЕНаЁЪ§ЕуКѓ7ЮЛЕФНсЙћЃЌЫћЪЧЪРНчЩЯЕквЛИіАбдВжмТЪЕФЪ§жЕМЦЫуЕНаЁЪ§ЕуКѓЕк7ЮЛЕФШЫЃЌетБШХЗжодчСЫдМ1000Фъ.ЩњЛюжаЃЌЮвУЧвВПЩвдЭЈЙ§ШчЯТЫцЛњФЃФтЪдбщРДЙРМЦ![]() ЕФжЕЃКдкЧјМф
ЕФжЕЃКдкЧјМф![]() ФкЫцЛњШЁ
ФкЫцЛњШЁ![]() ИіЪ§ЃЌЙЙГЩ
ИіЪ§ЃЌЙЙГЩ![]() ИіЪ§Жд
ИіЪ§Жд![]() ЃЌЩш
ЃЌЩш![]() ЃЌ
ЃЌ![]() Фмгы1ЙЙГЩЖлНЧШ§НЧаЮШ§БпЕФЪ§Жд
Фмгы1ЙЙГЩЖлНЧШ§НЧаЮШ§БпЕФЪ§Жд![]() га
га![]() ЖдЃЌдђЭЈЙ§ЫцЛњФЃФтЕФЗНЗЈЕУЕНЕФ
ЖдЃЌдђЭЈЙ§ЫцЛњФЃФтЕФЗНЗЈЕУЕНЕФ![]() ЕФНќЫЦжЕЮЊЃЈ ЃЉ
ЕФНќЫЦжЕЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ЁОД№АИЁПC
ЁОНтЮіЁП
ИљОндкЧјМф![]() ФкЫцЛњШЁ
ФкЫцЛњШЁ![]() ИіЪ§ЃЌдђга
ИіЪ§ЃЌдђга![]() ЃЌЪдбщЕФШЋВПНсЙћЙЙГЩвд1ЮЊБпГЄЕФе§ЗНаЮЃЌЦфУцЛ§ЮЊ1.вђЮЊ
ЃЌЪдбщЕФШЋВПНсЙћЙЙГЩвд1ЮЊБпГЄЕФе§ЗНаЮЃЌЦфУцЛ§ЮЊ1.вђЮЊ![]() ЃЌ
ЃЌ![]() Фмгы1ЙЙГЩЖлНЧШ§НЧаЮЃЌгЩгрЯвЖЈРэЕФМАШ§НЧаЮжЊЪЖЕУ
Фмгы1ЙЙГЩЖлНЧШ§НЧаЮЃЌгЩгрЯвЖЈРэЕФМАШ§НЧаЮжЊЪЖЕУ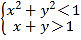 ЧѓЕУЯргІЕФУцЛ§ЃЌдйРћгУМИКЮИХаЭЕФИХТЪЙЋЪНЧѓНт.
ЧѓЕУЯргІЕФУцЛ§ЃЌдйРћгУМИКЮИХаЭЕФИХТЪЙЋЪНЧѓНт.
вРЬтга![]() ЃЌЪдбщЕФШЋВПНсЙћЙЙГЩвд1ЮЊБпГЄЕФе§ЗНаЮЃЌЦфУцЛ§ЮЊ1.
ЃЌЪдбщЕФШЋВПНсЙћЙЙГЩвд1ЮЊБпГЄЕФе§ЗНаЮЃЌЦфУцЛ§ЮЊ1.
вђЮЊ![]() ЃЌ
ЃЌ![]() Фмгы1ЙЙГЩЖлНЧШ§НЧаЮЃЌ
Фмгы1ЙЙГЩЖлНЧШ§НЧаЮЃЌ
гЩгрЯвЖЈРэЕФМАШ§НЧаЮжЊЪЖЕУ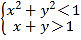 ЃЌ
ЃЌ
ЙЙГЩШчЭМвѕгАВПЗжЃЌ
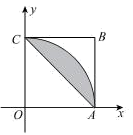
ЦфУцЛ§ЮЊ![]() ЃЌ
ЃЌ
гЩМИКЮИХаЭИХТЪМЦЫуЙЋЪНЕУ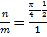 ЃЌ
ЃЌ
НтЕУ![]() .
.
ЙЪбЁЃКC


 ЬьЬьЯђЩЯПЮЪБЭЌВНбЕСЗЯЕСаД№АИ
ЬьЬьЯђЩЯПЮЪБЭЌВНбЕСЗЯЕСаД№АИ бєЙтПЮЬУЭЌВНСЗЯАЯЕСаД№АИ
бєЙтПЮЬУЭЌВНСЗЯАЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЃНЃЈ1ЉsinxЃЉex.
ЃЈ1ЃЉЧѓfЃЈxЃЉдкЧјМфЃЈ0ЃЌІаЃЉЕФМЋжЕЃЛ
ЃЈ2ЃЉжЄУїЃККЏЪ§gЃЈxЃЉЃНfЃЈxЃЉЉsinxЉ1дкЧјМфЃЈЉІаЃЌІаЃЉгаЧвжЛга3ИіСуЕуЃЌЧвжЎКЭЮЊ0.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕ![]() жаЃЌжБЯп
жаЃЌжБЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌ
ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌ![]() жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп
жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп![]() ЕФМЋзјБъЗНГЬЪЧ
ЕФМЋзјБъЗНГЬЪЧ![]() .
.
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉвбжЊЕу![]() ЃЌШєжБЯп
ЃЌШєжБЯп![]() гыЧњЯп
гыЧњЯп![]() НЛгкВЛЭЌЕФСНЕу
НЛгкВЛЭЌЕФСНЕу![]() ЃЌЕБ
ЃЌЕБ![]() зюДѓЪБЃЌЧѓГіжБЯп
зюДѓЪБЃЌЧѓГіжБЯп![]() ЕФжБНЧзјБъЗНГЬ.
ЕФжБНЧзјБъЗНГЬ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉЧѓКЏЪ§![]() ЕФЕЅЕїЧјМфКЭМЋжЕЃЛ
ЕФЕЅЕїЧјМфКЭМЋжЕЃЛ
ЃЈ2ЃЉШєЗНГЬ гаШ§ИіНтЃЌЧѓЪЕЪ§
гаШ§ИіНтЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЕу
жаЃЌЕу![]()
![]() дкЭждВ
дкЭждВ![]()
![]() ЩЯЃЌЧвЭждВЕФРыаФТЪЮЊ
ЩЯЃЌЧвЭждВЕФРыаФТЪЮЊ![]() .
.
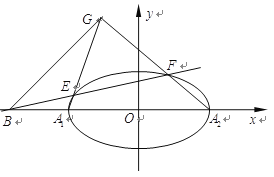
ЃЈ1ЃЉЧѓЭждВ![]() ЕФБъзМЗНГЬЃЛ
ЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉМЧЭждВЕФзѓЁЂгвЖЅЕуЗжБ№ЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() Лђ
Лђ![]() зївЛЬѕжБЯпНЛЭждВ
зївЛЬѕжБЯпНЛЭждВ![]() гк
гк![]() ЁЂ
ЁЂ![]() ЃЈВЛгы
ЃЈВЛгы![]() жиКЯЃЉСНЕуЃЌжБЯп
жиКЯЃЉСНЕуЃЌжБЯп![]() НЛгкЕу
НЛгкЕу![]() ЃЌМЧжБЯп
ЃЌМЧжБЯп![]() ЕФаБТЪЗжБ№ЮЊ
ЕФаБТЪЗжБ№ЮЊ![]() .
.
ЂйЖдгкИјЖЈЕФ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкЪЧЗёДцдквЛИіЖЈжЕ![]() ЪЙЕУ
ЪЙЕУ![]() КуГЩСЂЃЌШєДцдкЃЌЧѓГі
КуГЩСЂЃЌШєДцдкЃЌЧѓГі![]() жЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
жЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЙњЙХДњЪ§бЇУћжјЁЖЫуЗЈЭГзкЁЗжагаШчЯТЮЪЬтЃКЁАдЖЭћЮЁЮЁЫўЦпВуЃЌКьЙтЕуЕуБЖМгдіЃЌЙВЕЦШ§АйАЫЪЎвЛЃЌЧыЮЪМтЭЗМИеЕЕЦЃПЁБвтЫМЪЧЃКвЛзљ7ВуЫўЙВЙвСЫ381еЕЕЦЃЌЧвЯрСкСНВужаЕФЯТвЛВуЕЦЪ§ЪЧЩЯвЛВуЕЦЪ§ЕФ2БЖЃЌдђЫўЕФЖЅВуЙВгаЕЦЃЈ ЃЉ
A. 1еЕ B. 3еЕ C. 5еЕ D. 9еЕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙВЯэЕЅГЕгжГЦЮЊаЁЛЦГЕЃЌНќФъРДж№НЅзпНјСЫШЫУЧЕФЩњЛюЃЌвВГЩЮЊМѕЩйПеЦјЮлШОЃЌЛКНтГЧЪаНЛЭЈбЙСІЕФвЛжжживЊЪжЖЮЃЎЮЊЕїВщФГЕиЧјОгУёЖдЙВЯэЕЅГЕЕФЪЙгУЧщПіЃЌДгИУЕиЧјОгУёжаАДФъСфгУЫцЛњГщбљЕФЗНЪНЫцЛњГщШЁСЫ![]() ШЫНјааЮЪОэЕїВщЃЌЕУЕНет
ШЫНјааЮЪОэЕїВщЃЌЕУЕНет![]() ШЫЖдЙВЯэЕЅГЕЕФЦРМлЕУЗжЭГМЦЬюШыОЅвЖЭМЃЌШчЯТЫљЪОЃЈТњЗж
ШЫЖдЙВЯэЕЅГЕЕФЦРМлЕУЗжЭГМЦЬюШыОЅвЖЭМЃЌШчЯТЫљЪОЃЈТњЗж![]() ЗжЃЉЃК
ЗжЃЉЃК

ЃЈ1ЃЉевГіОгУёЮЪОэЕУЗжЕФжкЪ§КЭжаЮЛЪ§ЃЛ
ЃЈ2ЃЉЧыМЦЫует![]() ЮЛОгУёЮЪОэЕФЦНОљЕУЗжЃЛ
ЮЛОгУёЮЪОэЕФЦНОљЕУЗжЃЛ
ЃЈ3ЃЉШєдкГЩМЈЮЊ![]() ЗжЕФОгУёжаЫцЛњГщШЁ
ЗжЕФОгУёжаЫцЛњГщШЁ![]() ШЫЃЌЧѓЧЁга
ШЫЃЌЧѓЧЁга![]() ШЫГЩМЈГЌЙ§
ШЫГЩМЈГЌЙ§![]() ЗжЕФИХТЪЃЎ
ЗжЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЌЧв
ЃЌЧв![]() ЃЉ.
ЃЉ.
ЃЈ1ЃЉЧѓКЏЪ§![]() ЕФМЋжЕЕуЃЛ
ЕФМЋжЕЕуЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌжЄУїЃК
ЪБЃЌжЄУїЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЧњЯп
жаЧњЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌвд
ЮЊВЮЪ§ЃЉЃЌвд![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ![]() жсЕФе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌжБЯп
жсЕФе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌжБЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФЦеЭЈЗНГЬвдМАжБЯп
ЕФЦеЭЈЗНГЬвдМАжБЯп![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉНЋЧњЯп![]() ЯђзѓЦНвЦ2ИіЕЅЮЛЃЌдйНЋЧњЯп
ЯђзѓЦНвЦ2ИіЕЅЮЛЃЌдйНЋЧњЯп![]() ЩЯЕФЫљгаЕуЕФКсзјБъЫѕЖЬЮЊдРДЕФ
ЩЯЕФЫљгаЕуЕФКсзјБъЫѕЖЬЮЊдРДЕФ![]() ЃЌЕУЕНЧњЯп
ЃЌЕУЕНЧњЯп![]() ЃЌЧѓЧњЯп
ЃЌЧѓЧњЯп![]() ЩЯЕФЕуЕНжБЯп
ЩЯЕФЕуЕНжБЯп![]() ЕФОрРыЕФзюаЁжЕ.
ЕФОрРыЕФзюаЁжЕ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com