
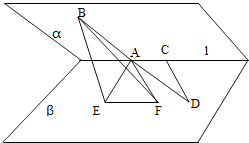
【题目】已知二面角α﹣l﹣β为60°,ABα,AB⊥l,A为垂足,CDβ,C∈l,∠ACD=135°,则异面直线AB与CD所成角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:如图,过A点做AE⊥l,使BE⊥β,垂足为E,过点A做AF∥CD,过点E做EF⊥AE,连接BF,
∵AE⊥l∴∠EAC=90°
∵CD∥AF又∠ACD=135°
∴∠FAC=45°∴∠EAF=45°
在Rt△BEA中,设AE=a,则AB=2a,BE= ![]() a,
a,
在Rt△AEF中,则EF=a,AF= ![]() a,
a,
在Rt△BEF中,则BF=2a,
∴异面直线AB与CD所成的角即是∠BAF,
∴cos∠BAF= ![]() =
= ![]() =
= ![]() .
.
所以答案是:B.
【考点精析】通过灵活运用异面直线及其所成的角,掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知集合M={1,2,3,4,5,6,7,8,9,10,11,12},以下命题正确的序号是 .
①如果函数f(x)=x(x﹣a1)(x﹣a2)…(x﹣a7),其中ai∈M(i=1,2,3,…,7),那么f′(0)的最大值为127 .
②数列{an}满足首项a1=2,ak+12﹣ak2=2,k∈N* , 当n∈M且n最大时,数列{an}有2048个.
③数列{an}(n=1,2,3,…,8)满足a1=5,a8=7,|ak+1﹣ak|=2,k∈N* , 如果数列{an}中的每一项都是集合M的元素,则符合这些条件的不同数列{an}一共有33个.
④已知直线amx+any+ak=0,其中am , an , ak∈M,而且am<an<ak , 则一共可以得到不同的直线196条.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1中,M,N分别为AB,BC的中点.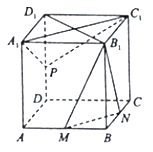
(1)求证:平面B1MN⊥平面BB1D1D;
(2)当点P在DD1上运动时,是否都有MN∥平面A1C1P,证明你的结论;
(3)若P是D1D的中点,试判断PB与平面B1MN是否垂直?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线mx+ ![]() y﹣1=0在y轴上的截距是﹣1,且它的倾斜角是直线
y﹣1=0在y轴上的截距是﹣1,且它的倾斜角是直线 ![]() =0的倾斜角的2倍,则( )
=0的倾斜角的2倍,则( )
A.m=﹣ ![]() ,n=﹣2
,n=﹣2
B.m= ![]() ,n=2
,n=2
C.m= ![]() ,n=﹣2
,n=﹣2
D.m=﹣ ![]() ,n=2
,n=2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线C:ρ2﹣2ρcosθ﹣8=0 曲线E: ![]() (t是参数)
(t是参数)
(1)求曲线C的普通方程,并指出它是什么曲线.
(2)当k变化时指出曲线K是什么曲线以及它恒过的定点并求曲线E截曲线C所得弦长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x2﹣tcosx.若其导函数f′(x)在R上单调递增,则实数t的取值范围为( )
x2﹣tcosx.若其导函数f′(x)在R上单调递增,则实数t的取值范围为( )
A.[﹣1,﹣ ![]() ]
]
B.[﹣ ![]() ,
, ![]() ]
]
C.[﹣1,1]
D.[﹣1, ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com