Question

某人有楼房一幢，室内面积共180㎡,拟分隔两类房间作为旅游客房．大每间面积为18㎡，可住游客5名，每名游客每天住宿费为40元；小房间每间面积为15㎡，可住游客3名，每名游客每天住宿费为50元；装修大房间每间需1000元，装修小房间每间需600元．如果他只能筹款8000元用于装修，且游客能住满客房，他应隔出大房间和小房间各多少间，能获得最大收益？

Answer 1

其一是将楼房室内全部隔出小房间１２间；其二是隔出大房间３间，小房间８间

解析:

将已知数据列成下表:

房间类型	装修费 （元）	面积 （㎡）	利润 （元）
大房间（间）	1000	18	5×40
小房间（间）	600	15	3×50
限额	8000	180

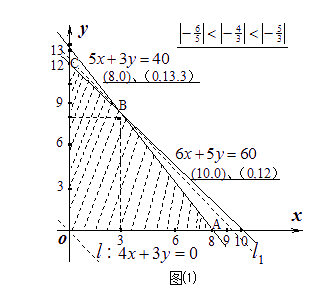设应隔出大、小房间分别为x,y间，此时收益为z元，则

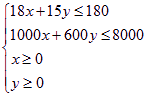
将上述不等式组化为

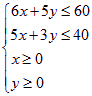
作出可行域，如图⑴，作直线l:200x+150y=0,即l:4x+3y=0.

将直线l向右平移，得到经过可行域的点B，且距原点最远的直线l_1.

     解方程组

得最优解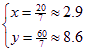           　

     但是房间的间数为整数，所以，应找到是整数的最优解．

当x=3时，代入5x+3y=40中，得，得整点（3，8），此时z=200×3＋150×8=1800（元）;

当x=2时,代入6x+5y=60中，得，得整点（2，9），此时z=200×2＋150×9=1750（元）；

当x=1时,代入6x+5y=60中，得，得整点（1，10）,

此时z=200×1＋150×10=1700（元）；

当x=0时,代入6x+5y=60中，得，得整点（0，12），此时z=150×12=1800（元）．

由上①～④知，最优整数解为（0，12）和（3，8）．

答：有两套分隔房间的方案：其一是将楼房室内全部隔出小房间１２间；其二是隔出大房间３间，小房间８间，两套方案都能获得最大收益为１８００元．