
(本题满分14分)
已知函数f(x)=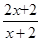 ,若数列
,若数列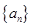 ,
,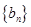 满足
满足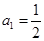 ,
, ,
,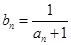
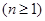 ,
,
(1)求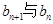 的关系,并求数列
的关系,并求数列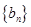 的通项公式;
的通项公式;
(2)记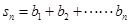 ,
若
,
若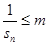 恒成立.求
恒成立.求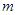 的最小值.
的最小值.
(1) bn= (
(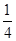 )n-1+
)n-1+ .(2)
m的最小值为
.(2)
m的最小值为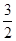 。
。
【解析】
试题分析:(1)根据递推关系和已知的所求解的,构造那个结构特点的关系式,进而得到结论。(2)利用第一问的结论得到数列{bn- }是首项b1-
}是首项b1- =
= ,公比为
,公比为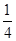 的等比数列,进而得到通项公式,并求解和式。
的等比数列,进而得到通项公式,并求解和式。
解:(1)∵ ,∴
,∴ .………2
.………2
又 ,∴
,∴ ,
,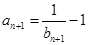 .………3
.………3
∴代入化简得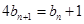 ,………4 ∴
,………4 ∴
∴ ,………6∴数列{bn-
,………6∴数列{bn- }是首项b1-
}是首项b1- =
= ,公比为
,公比为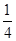 的等比数列,
的等比数列,
∴bn- =
= (
(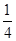 )n-1,bn=
)n-1,bn= (
(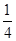 )n-1+
)n-1+ .………………8
.………………8
(2)Sn= =
=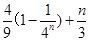 …10
…10
∴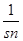 =
= ≤
≤ =
=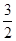 ,………12∴
,………12∴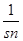 的最大值为
的最大值为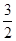 ,又
,又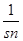 ≤m,
≤m,
∴m的最小值为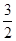 ………………………14
………………………14
考点:本试题主要考查了数列通项公式和前n项和的求解的综合运用。
点评:解决该试题的关键是对于分式递推式,采用取倒数的方法得到递推关系式,并能结合分组求和的思想得到数列的 前n项和问题。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| π |
| 3 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,![]() 为
为![]() 上的点,且BF⊥平面ACE.
上的点,且BF⊥平面ACE.
(1)求证:AE⊥BE;(2)求三棱锥D-AEC的体积;(3)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三上学期期中考试数学 题型:解答题
(本题满分14分)已知集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}
(Ⅰ)若A B=[0,3],求实数m的值
B=[0,3],求实数m的值
(Ⅱ)若A CRB,求实数m的取值范围
CRB,求实数m的取值范围
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三上学期第三次月考理科数学卷 题型:解答题
(本题满分14分)
已知点 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 作
作 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。
(1)求动点 的轨迹方程;
的轨迹方程;
(2)已知点 ,在动点
,在动点 的轨迹上是否存在两个不重合的两点
的轨迹上是否存在两个不重合的两点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2014届江西省高一第二学期入学考试数学 题型:解答题
(本题满分14分)已知函数 .
.
(1)求函数 的定义域;
的定义域;
(2)判断 的奇偶性;
的奇偶性;
(3)方程 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使

 ;如果没有,请说明理由?(注:区间的长度为
;如果没有,请说明理由?(注:区间的长度为 ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com