点P是直线l:x-y-2=0上的动点,点A,B分别是圆C1:(x+3)2+(y-1)2=4和圆C2:x2+(y-3)2=1上的两个动点,则|PA|+|PB|的最小值为 .
【答案】
分析:根据题意,算出圆C
2关于直线l对称的圆C'方程为(x-5)
2+(y+2)
2=1.当点P位于线段C
1C'上时,线段AB'长是圆C
1与圆C'上两个动点之间的距离最小值,由此结合对称的知识与两点间的距离公式加以计算,即可得出|PA|+|PB|的最小值.
解答:解:设圆C'是圆C
2:x
2+(y-3)
2=1关于直线l对称的圆
可得C'(5,-2),圆C'方程为(x-5)
2+(y+2)
2=1

可得当点P位于线段C
1C'上时,线段AB'长是圆C
1与圆C'上两个动点之间的距离最小值
B'关于直线l对称的点在圆C
2上,由平几知识得当圆C
2上的
动点B与该点重合时,|PA|+|PB|达到最小值
∵|C
1C'|=

=
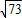
,
可得|AB'|=|C
1C'|-r
1-r
2=

因此,|PA|+|PB|的最小值等于|AB'|=

故答案为:
 点评:
点评:本题给出直线l与两个定圆,求圆上两个点A、B与直线l上动点P的距离之和的最小值,着重考查了直线的方程、圆的方程和直线与圆的位置关系等知识,属于中档题.


 =
=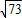 ,
,




 (2011•武昌区模拟)如图,已知点P是圆上C:x2+(y-2
(2011•武昌区模拟)如图,已知点P是圆上C:x2+(y-2