

图2-3-25
思路解析:由于E、F为中点,所以猜想M也是中点.
答案:当![]() =1时,能使D1M⊥平面EFB1,证明如下:
=1时,能使D1M⊥平面EFB1,证明如下:
当M为B1B中点时,在平面AA1B1B内有△A1MB1≌△B1EB,
∴∠B1A1M=∠BB1E.而∠B1MA1+∠B1A1M=90°,
∴∠B1MA1+∠BB1E=90°.∴A1M⊥B1E.
∵D1A1⊥平面AA1B1B,B1E![]() 平面AA1B1B,
平面AA1B1B,
∴D1A1⊥B1E.由于A1M∩D1A1=A1,
∴B1E⊥平面A1MD1.∵D1M![]() 平面A1MD1,
平面A1MD1,
∴B1E⊥D1M.同理,连结C1M,可证明B1F⊥D1M.
∵B1E∩B1F=B1,∴D1M⊥平面EFB1.
绿色通道:
(1)猜想要和题目中的点的性质相联系,见中点找中点是常见的解题策略.
(2)平面内证两线垂直的方法还可通过三角形中某两个角的和为直角来判断.


 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
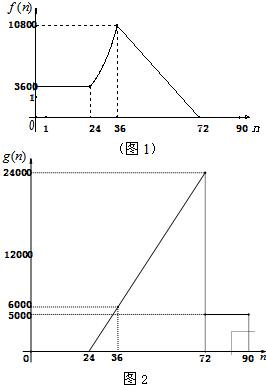 2010年上海世博会组委会为保证游客参观的顺利进行,对每天在各时间段进入园区和离开园区的人数作了一个模拟预测.为了方便起见,以10分钟为一个计算单位,上午9点10分作为第一个计算人数的时间,即n=1;9点20分作为第二个计算人数的时间,即n=2;依此类推…,把一天内从上午9点到晚上24点分成了90个计算单位.
2010年上海世博会组委会为保证游客参观的顺利进行,对每天在各时间段进入园区和离开园区的人数作了一个模拟预测.为了方便起见,以10分钟为一个计算单位,上午9点10分作为第一个计算人数的时间,即n=1;9点20分作为第二个计算人数的时间,即n=2;依此类推…,把一天内从上午9点到晚上24点分成了90个计算单位.
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省豫南九校高三第四次联考理科数学 题型:解答题
(本小题满分12分)
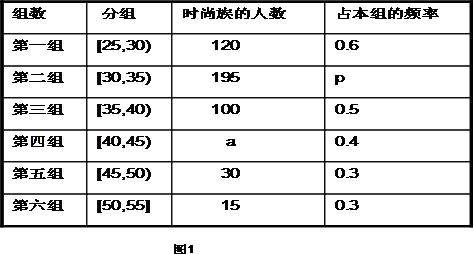
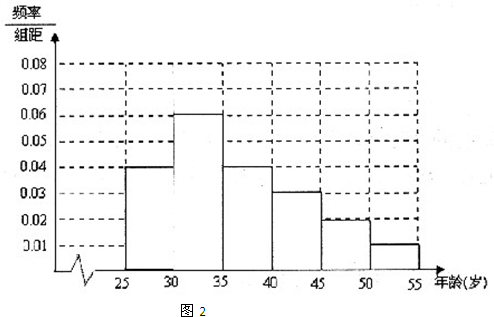
某高中社团进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”。通过调查分别得到如图1所示统计表如图2所示各年龄段人数频率分布直方图:

请完成下列问题:
(1)补全频率分布直方图,并求 的值;
的值;
(2)从 岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络时尚达人大赛,其中选取3人作为领队,求选取的3名领队年龄在
岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络时尚达人大赛,其中选取3人作为领队,求选取的3名领队年龄在 岁的人数为X,求X的分布列和期望E(X)。
岁的人数为X,求X的分布列和期望E(X)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com