【题目】在平面直角坐标系xOy中，抛物线y2=4x的焦点为F，抛物线上有三个动点A,B,C.
（1）若
，求
；
（2）若
，AB的垂直平分线经过一个定点Q，求△QAB面积的最大值.
暑假作业海燕出版社系列答案科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
已知曲线
的极坐标方程为
，直线
，直线 
．以极点
为原点，极轴为
轴的正半轴建立平面直角坐标系．
（1）求直线
，
的直角坐标方程以及曲线的参数方程；
（2）已知直线与曲线交于
两点，直线与曲线交于
两点，求
的面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】篮球场上有5个人在练球，其战术是由甲开始发球（第1次传球），经过6次传球跑动后（中途每人的传接球机会均等），回到甲，由甲投3分球，其不同的传球方式有（ ）种.
A. 4 100 B. 1 024 C. 976 D. 820
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为测试特斯拉汽车的百米加速时间，研发人员记录了汽车在
取
、
、
、
、
、
、
时刻的位移，并对数据做了初步处理，得到图
.同时，令
，得到数据图
，现画出
与，与
的散点图.
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
累加 |
|
|
|
| 累加 |
|
|
|
|
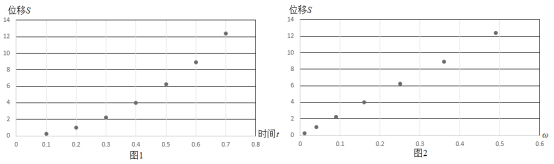
（1）根据散点图判断，与，与哪两个量之间线性相关程度更强？（直接给出判断即可）；
（2）根据（1）的结果选择线性相关程度更强的两个量，建立相应的回归直线方程；
（3）根据（2）的结果预计特斯拉汽车百米加速需要的时间.
附：对于一组数据
、
、
、
，其回归直线
的斜率和截距的最小二乘估计分别为：
，
.
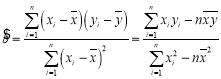查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，其图象的一个对称中心是
，将
的图象向左平移
个单位长度后得到函数
的图象.
（1）求函数的解析式；
（2）若对任意
，当
时，都有
，求实数
的最大值；
（3）若对任意实数
在
上与直线
的交点个数不少于6个且不多于10个，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知空间四边形ABCD，∠BAC＝
，AB＝AC＝2
，BD＝CD＝6，且平面ABC⊥平面BCD，则空间四边形ABCD的外接球的表面积为( )
A. 60π B. 36π C. 24π D. 12π
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了调查一款电视机的使用时间，研究人员对该款电视机进行了相应的测试，将得到的数据统计如下图所示：
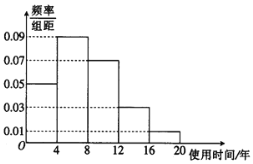
并对不同年龄层的市民对这款电视机的购买意愿作出调查，得到的数据如下表所示：
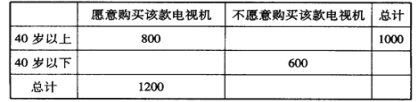
（1）根据图中的数据，试估计该款电视机的平均使用时间；
（2）根据表中数据，判断是否有99．9％的把握认为“愿意购买该款电视机”与“市民的年龄”有关；
（3）若按照电视机的使用时间进行分层抽样，从使用时间在[0，4）和[4，20]的电视机中抽取5台，再从这5台中随机抽取2台进行配件检测，求被抽取的2台电视机的使用时间都在[4，20]内的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在2018年俄罗斯世界杯期间,莫斯科的部分餐厅经营了来自中国的小龙虾,这些小龙虾标有等级代码.为得到小龙虾等级代码数值
与销售单价
之间的关系,经统计得到如下数据：
等级代码数值 | 38 | 48 | 58 | 68 | 78 | 88 |
销售单价 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
（1）已知销售单价与等级代码数值之间存在线性相关关系,求关于的线性回归方程(系数精确到0.1)；
（2）若莫斯科某餐厅销售的中国小龙虾的等级代码数值为98，请估计该等级的中国小龙虾销售单价为多少元？
参考公式：对一组数据
,
，····
,其回归直线
的斜率和截距最小二乘估计分别为：
,
.
参考数据：
,
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
