| 北京市房山区2011年高三上学期期末统练试卷(数学理).doc |
| |
| | (本小题共13分) 某同学设计一个摸奖游戏:箱内有红球3个,白球4个,黑球5个.每次任取一个,有放回地抽取3次为一次摸奖.至少有两个红球为一等奖,记2分;红、白、黑球各一个为二等奖,记1分;否则没有奖,记0分. (I)求一次摸奖中一等奖的概率; (II)求一次摸奖得分的分布列和期望.
(本小题共13分) 解:(I)每次有放回地抽取,取到红球的概率为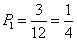 ;取到白球的概率为 ;取到白球的概率为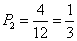 ;取到 ;取到 黑球的概率为 ; -------3分 ; -------3分 一次摸奖中一等奖的概率为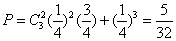 . ---------5分 . ---------5分 (II)设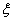 表示一次摸奖的得分,则 表示一次摸奖的得分,则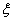 可能的取值为0,1,2. --------------6分 可能的取值为0,1,2. --------------6分 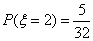 ; ;
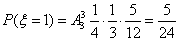 ; --------8分 ; --------8分
 ---10分 ---10分
 一次摸奖得分 一次摸奖得分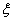 的分布列为 的分布列为
----------11分 期望为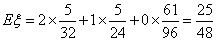 . ----------13分 . ----------13分
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
| 北京市房山区2011年高三上学期期末统练试卷(数学理).doc | | | | | (本小题共13分) 在中,角A、B、C的对边分别为、、,角A、B、C成等差数列,,边的长为. (I)求边的长; (II)求的面积.
查看答案和解析>>
科目:高中数学
来源:
题型:
| 北京市房山区2011年高三上学期期末统练试卷(数学理).doc | | | | | (本小题共14分) 已知数列中,,设. (Ⅰ)试写出数列的前三项; (Ⅱ)求证:数列是等比数列,并求数列的通项公式; (Ⅲ)设的前项和为,求证:.
查看答案和解析>>
科目:高中数学
来源:
题型:
| 北京市房山区2011年高三上学期期末统练试卷(数学理).doc | | | | | (本小题共14分) 设函数. (Ⅰ)求函数的定义域及其导数; (Ⅱ)当时,求函数的单调区间; (Ⅲ)当时,令,若在上的最大值为,求实数的值.
查看答案和解析>>
科目:高中数学
来源:
题型:
| 北京市房山区2011年高三上学期期末统练试卷(数学理).doc | | | | | 如图所示,是定义在区间()上的奇函数,令,并有关于函数的四个论断: ①若,对于内的任意实数(),恒成立; 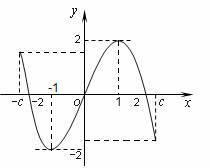 ②函数是奇函数的充要条件是; ②函数是奇函数的充要条件是;
③若,,则方程必有3个实数根; ④,的导函数有两个零点; 其中所有正确结论的序号是 .
查看答案和解析>>
科目:高中数学
来源:
题型:
| 北京市房山区2011年高三上学期期末统练试卷(数学理).doc | | | | | (本小题共13分) 已知正方形ABCD的边长为1,.将正方形ABCD沿对角线折起,使,得到三棱锥A—BCD,如图所示. (I)若点M是棱AB的中点,求证:OM∥平面ACD; 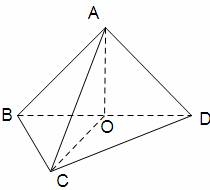 (II)求证:; (II)求证:;
(III)求二面角的余弦值.
查看答案和解析>>
| | | | | | | | | | | |
