
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() 是等腰三角形,
是等腰三角形,![]() ,
,![]() 是
是![]() 的一个三等分点(靠近点
的一个三等分点(靠近点![]() ),
),![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.

(1)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)求二面角![]() 的正切值.
的正切值.
【答案】(1)![]() ;
;
(2)![]() .
.
【解析】
(1)建立空间直角坐标系,设![]() ,根据题意确定
,根据题意确定![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,找点P,D,E,F坐标,确定直线
,找点P,D,E,F坐标,确定直线![]() 与
与![]() 的方向向量,根据异面直线
的方向向量,根据异面直线![]() 与
与![]() 所成角
所成角![]() 满足
满足![]() ,求解,即可.
,求解,即可.
(2)根据(1)的点坐标,求平面![]() 的一个法向量为
的一个法向量为![]() 和平面
和平面![]() 的一个法向量为
的一个法向量为![]() .由题意可知二面角
.由题意可知二面角![]() 为锐角,根据
为锐角,根据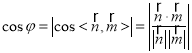 求出
求出![]() ,从而计算
,从而计算![]() ,即可.
,即可.
(1)![]() 底面
底面![]() 是矩形,
是矩形,![]() 平面
平面![]()
![]()
![]() ,
,![]() ,
,![]()
以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴建立如图所示的空间直角坐标系.
轴建立如图所示的空间直角坐标系.
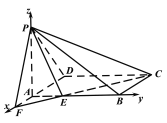
因为![]() 是
是![]() 的一个三等分点(靠近点
的一个三等分点(靠近点![]() ),所以
),所以![]() ,
,![]() .
.
因为![]() 是等腰三角形,且
是等腰三角形,且![]() ,所以
,所以![]() .
.
不妨设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
又由平行线分线段成比例,得![]() ,所以
,所以![]() .
.
所以点![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() .
.
设异面直线![]() 与
与![]() 所成角为
所成角为![]() ,
,
则 .
.
所以异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
(2)建系,求点的坐标同(1),则![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则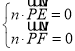 ,得
,得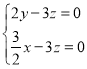 .
.
令![]() ,得平面
,得平面![]() 的一个法向量为
的一个法向量为![]() ;
;
又易知平面![]() 的一个法向量为
的一个法向量为![]() .
.
设二面角![]() 的大小为
的大小为![]() ,由题意得
,由题意得![]() 为锐角,
为锐角,
所以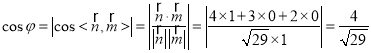 ,则
,则![]() .
.
所以二面角![]() 的正切值为
的正切值为![]() .
.


科目:高中数学 来源: 题型:
【题目】经过多年的运作,“双十一”抢购活动已经演变成为整个电商行业的大型集体促销盛宴.为迎接2018年“双十一”网购狂欢节,某厂家拟投入适当的广告费,对网上所售产品进行促销.经调查测算,该促销产品在“双十一”的销售量p万件与促销费用x万元满足![]() (其中
(其中![]() ,a为正常数).已知生产该产品还需投入成本
,a为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),每一件产品的销售价格定为
万元(不含促销费用),每一件产品的销售价格定为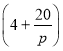 元,假定厂家的生产能力完全能满足市场的销售需求.
元,假定厂家的生产能力完全能满足市场的销售需求.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大?并求出最大利润的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度得到
个单位长度得到![]() 的图象,若
的图象,若![]() 的对称中心为坐标原点,则关于函数
的对称中心为坐标原点,则关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 的最小正周期为
的最小正周期为![]() ②若
②若![]() 的最大值为2,则
的最大值为2,则![]()
③![]() 在
在![]() 有两个零点 ④
有两个零点 ④![]() 在区间
在区间![]() 上单调
上单调
其中所有正确结论的标号是( )
A.①③④B.①②④C.②④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若函数![]() 的图象经过变换
的图象经过变换![]() 后所得的图象对应的函数与
后所得的图象对应的函数与![]() 的值域相同,则称变换
的值域相同,则称变换![]() 是
是![]() 的同值变换,下面给出了四个函数与对应的变换:①
的同值变换,下面给出了四个函数与对应的变换:①![]() ,
, ![]() 将函数
将函数![]() 的图象关于直线
的图象关于直线![]() 作对称变换;②
作对称变换;②![]() ,
, ![]() 将函数
将函数![]() 的图象关于
的图象关于![]() 轴作对称变换;③
轴作对称变换;③![]() ,
, ![]() 将函数
将函数![]() 的图象关于点
的图象关于点![]() 作对称变换;④
作对称变换;④![]() ,
,![]() 将函数
将函数![]() 的图象关于点
的图象关于点![]() 作对称变换.其中
作对称变换.其中![]() 是
是![]() 的同值变换的有__________(写出所有符合题意的序号)
的同值变换的有__________(写出所有符合题意的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.若曲线
轴正半轴为极轴建立极坐标系.若曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 点的极坐标为
点的极坐标为![]() ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线![]() 经过点
经过点![]() ,且倾斜角为
,且倾斜角为![]() .
.
(1)写出曲线![]() 的直角坐标方程以及点
的直角坐标方程以及点![]() 的直角坐标;
的直角坐标;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为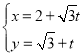 (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为
轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程及曲线C的直角坐标方程;
的极坐标方程及曲线C的直角坐标方程;
(2)若![]() 是直线
是直线![]() 上的一点,
上的一点,![]() 是曲线C上的一点,求
是曲线C上的一点,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com