
分析 (Ⅰ)根据函数奇偶性的定义进行判断;
(Ⅱ)求出函数g(x)的表达式,结合函数单调性的定义进行判断.
解答 解:(Ⅰ)当k=3时,f(x)=x3,则f(-x)=(-x)3=-x3=-f(x),
则函数f(x)为奇函数;
(Ⅱ)当k=1时,函数g(x)=f(x)+$\frac{4}{f(x)}$=x+$\frac{4}{x}$,
则函数在间(0,2]上的单调递减,
证明:0<x1<x2≤2,
则$f({x_1})-f({x_2})={x_1}+\frac{4}{x_1}-{x_2}-\frac{4}{x_2}=({x_1}-{x_2})+\frac{{4({x_2}-{x_1})}}{{{x_1}{x_2}}}=({x_1}-{x_2})(1-\frac{4}{{{x_1}{x_2}}})$=(x1-x2)•$\frac{{x}_{1}{x}_{2}-4}{{x}_{1}{x}_{2}}$,
∵0<x1<x2≤2,
∴x1-x2<0,0<x1x2<4,
∴f(x1)-f(x2)>0,
∴函数g(x)在区间(0,2]上的单调递减.
点评 本题主要考查函数奇偶性和单调性的判断和应用,结合函数奇偶性和单调性的定义是解决本题的关键.


科目:高中数学 来源: 题型:解答题
 在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹记作曲线C.
在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹记作曲线C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
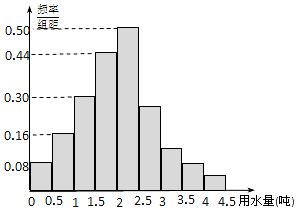 某地区100位居民的人均月用水量(单位:t)的频率分布直方图及频数分布表如下:
某地区100位居民的人均月用水量(单位:t)的频率分布直方图及频数分布表如下:| 分组 | 频数 |
| [0,0.5) | 4 |
| [0.5,1) | 8 |
| [1,1.5) | 15 |
| [1.5,2) | 22 |
| [2,2.5) | 25 |
| [2.5,3) | 14 |
| [3,3.5) | 6 |
| [3.5,4) | 4 |
| [4,4.5) | 2 |
| 合计 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | -$\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4) | B. | (2,4) | C. | (0,2)∪(2,4) | D. | (-∞,2)∪(2,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com