【题目】如图，空间几何体由两部分构成，上部是一个底面半径为1，高为2的圆锥，下部是一个底面半径为1，高为2的圆柱，圆锥和圆柱的轴在同一直线上，圆锥的下底面与圆柱的上底面重合，点
是圆锥的顶点，
是圆柱下底面的一条直径，
、
是圆柱的两条母线，
是弧的中点.
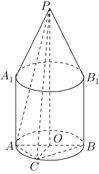
（1）求异面直线
与
所成的角的大小；
（2）求点
到平面
的距离.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】某工厂因排污比较严重，决定着手整治，一个月时污染度为
，整治后前四个月的污染度如下表：
月数 |
|
|
|
| … |
污染度 |
|
|
|
| … |
污染度为
后，该工厂即停止整治，污染度又开始上升，现用下列三个函数模拟从整治后第一个月开始工厂的污染模式：
，
，
，其中
表示月数，
、
、
分别表示污染度．
（1）问选用哪个函数模拟比较合理，并说明理由；
（2）若以比较合理的模拟函数预测，整治后有多少个月的污染度不超过![](http://thumb.1010pic.com/questionBank/Upload/2020/05/31/06/c7ade7a2/SYS202005310600492128280640_ST/SYS202005310600492128280640_ST.001.png"){kind=small}
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某环线地铁按内、外环线同时运行，内、外环线的长均为30千米（忽略内、外环线长度差异）．
（1）当9列列车同时在内环线上运行时，要使内环线乘客最长候车时间为10分钟，求内环线列车的最小平均速度；
（2）新调整的方案要求内环线列车平均速度为25千米/小时，外环线列车平均速度为30千米/小时．现内、外环线共有18列列车全部投入运行，要使内外环线乘客的最长候车时间之差不超过1分钟，向内、外环线应各投入几列列车运行？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
，
为两非零有理数列（即对任意的
，
均为有理数），
为一无理数列（即对任意的，
为无理数）．
（1）已知
，并且
对任意的
恒成立，试求的通项公式．
（2）若
为有理数列，试证明：对任意的，
恒成立的充要条件为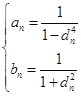
．
（3）已知
，
，对任意的，
恒成立，试计算
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
为定义在实数集
上的函数，把方程
称为函数
的特征方程，特征方程的两个实根
、
（
），称为的特征根.
（1）讨论函数的奇偶性，并说明理由；
（2）已知
为给定实数，求
的表达式；
（3）把函数
，
的最大值记作
，最小值记作
，研究函数，的单调性，令
，若
恒成立，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
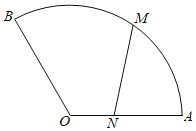
【题目】某公园草坪上有一扇形小径（如图）,扇形半径为
,中心角为
,甲由扇形中心
出发沿
以每秒2米的速度向
快走,同时乙从出发,沿扇形弧以每秒
米的速度向
慢跑,记
秒时甲、乙两人所在位置分别为
,
，通过计算
，判断下列说法是否正确：
（1）当
时，函数
取最小值；
（2）函数
在区间
上是增函数；
（3）若
最小，则
；
（4）
在
上至少有两个零点；
其中正确的判断序号是______（把你认为正确的判断序号都填上）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，其中无理数
.
（Ⅰ）若函数
有两个极值点，求
的取值范围；
（Ⅱ）若函数
的极值点有三个，最小的记为
，最大的记为
，若
的最大值为
，求
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
