练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知集合P＝{x|－2≤x≤10}，Q＝{x|1－m≤x≤1＋m}．

    (1)求集合RP；

    (2)若PQ，求实数m的取值范围；

    (3)若P∩Q＝Q，求实数m的取值范围．

    【答案】(1) RP＝{x|x<－2或x>10}； (2) [9，＋∞);（3）(－∞，3]．

    【解析】试题分析：（1）根据数轴可得结合补集（2）根据数轴可得实数m满足的条件，解不等式可得m的取值范围；（3）由P∩Q＝Q得，QP，再分空间与非空讨论，结合数轴可得实数m满足的条件，解不等式可得m的取值范围

    试题解析：(1)RP＝{x|x<－2或x>10}；

    (2)由PQ，需得m≥9，即实数m的取值范围为[9，＋∞);

    (3)由P∩Q＝Q得，QP，

    ①当1－m>1＋m，即m<0时，Q＝，符合题意；

    ②当1－m≤1＋m，即m≥0时，需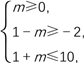

    得0≤m≤3；

    综上得：m≤3，即实数m的取值范围为(－∞，3]．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数．

    （1）若当时，函数的图象恒在直线上方，求实数的取值范围；

    （2）求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,设铁路长为,且,为将货物从运往,现在上的距点为的点处修一公路至,已知单位距离的铁路运费为,公路运费为.

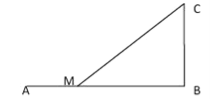
    （1）将总运费表示为的函数；

    （2）如何选点才使总运费最小？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【2016高考四川文科】已知数列{ }的首项为1， 为数列的前n项和， ，其中q>0， .

    （Ⅰ）若 成等差数列，求的通项公式；

    （Ⅱ）设双曲线 的离心率为 ，且 ，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，直线的参数方程为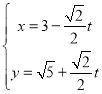（为参数），在极坐标系（与直角坐标系取相同的长度单位，且以原点为极点，以轴正半轴为极轴）中，圆的方程为．

    （1）求圆的直角坐标方程；

    （2）设圆与直线交于点，若点的坐标为，求．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】求下列函数解析式：

    (1)已知是一次函数，且满足3－＝，求；

    (2)已知＝，求的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求函数在上的最大值；

    （2）令，若在区间上为单调递增函数，求的取值范围；

    （3）当时，函数的图象与轴交于两点且，又是的导函数.若正常数满足条件.证明： <0.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中均为实数， 为自然对数的底数．

    （I）求函数的极值；

    （II）设，若对任意的，

    恒成立，求实数的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义域为的函数是奇函数．

    （1）求的值；

    （2）猜测的单调性，并用定义证明；

    （3）若对任意，不等式恒成立，求实数的取值范围．

    查看答案和解析>>

    同步练习册答案