
分析 (Ⅰ)当a<2时,写出分段函数,利用函数f(x)的最小值为1,求实数a的值.
(Ⅱ)由条件求得(2x+4)•(x-a)≤0,分类讨论求得x的范围.
解答 解:(Ⅰ)函数f(x)=|2x+4|+|x-a|的零点为-2和a,
当a<-2时,f(x)=$\left\{\begin{array}{l}{-3x-4+a,x<a}\\{-x-4-a,a≤x≤-2}\\{3x+4-a,x>-2}\end{array}\right.$,
∴f(x)min=f(-2)=2-4-a=1,得a=-3<-2(合题意),即a=-3.
(Ⅱ)由f(x)=|2x+4|+|x-a|,可得|2x+4|+|x-a|=|x+a+4|.
由于|2x+4|+|x-a|≥|x+a+4|,当且仅当(2x+4)•(x-a)≤0时,取等号.
当a=-2时,可得x=-2,故x的范围为{2};当a>-2时,可得-2≤x≤a,故x的范围为[-2,a];
当a<-2时,可得a≤x≤-2,故x的范围为[a,-2].
点评 本题主要考查带有绝对值的函数,绝对值不等式的解法,体现了转化、数形结合、分类讨论的数学思想,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
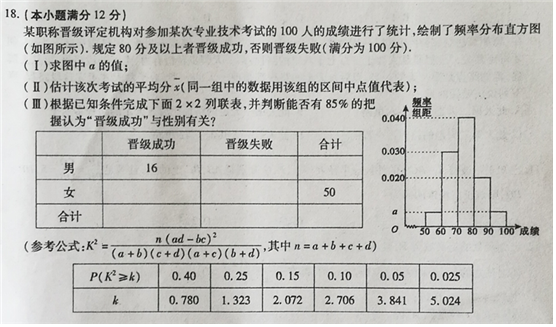
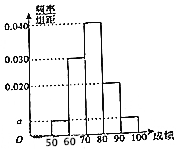 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).| 晋级成功 | 晋级失败 | 合计 | |
| 男 | 16 | ||
| 女 | 50 | ||
| 合计 |
| P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 公元263年左右,我国数学家刘徽发现,当圆内接正多边形的边数无限增加时,正多边形的周长可无限逼近圆的周长,并创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率,利用刘徽的割圆术设计的程序框图如图所示,若输出的n=96,则判断框内可以填入( )(参考数据:sin7.5°≈0.1305,sin3.75°≈0.06540,sin1.875°≈0.03272)
公元263年左右,我国数学家刘徽发现,当圆内接正多边形的边数无限增加时,正多边形的周长可无限逼近圆的周长,并创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率,利用刘徽的割圆术设计的程序框图如图所示,若输出的n=96,则判断框内可以填入( )(参考数据:sin7.5°≈0.1305,sin3.75°≈0.06540,sin1.875°≈0.03272)| A. | p≤3.14 | B. | p≥3.14 | C. | p≥3.1415 | D. | p≥3.1415926 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\sqrt{2}$-1,$\sqrt{2}$+1] | B. | [1,$\sqrt{2}$] | C. | [$\sqrt{2}$,$\sqrt{3}$] | D. | [$\sqrt{2}$-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{10}}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com