
【题目】某中超足球队的后卫线上一共有7名球员,其中3人只能打中后卫,2人只能打边后卫,2人既能打中后卫又能打边后卫,主教练决定选派4名后卫上场比赛,假设可以随机选派球员.
(1)在选派的4人中至少有2人能打边后卫的概率;
(2)在选派的4人中既能打中后卫又能打边后卫的人数![]() 的分布列与期望.
的分布列与期望.
科目:高中数学 来源: 题型:
【题目】如图1,已知四边形BCDE为直角梯形,![]() ,
,![]() ,且
,且![]() ,A为BE的中点
,A为BE的中点![]() 将
将![]() 沿AD折到
沿AD折到![]() 位置
位置![]() 如图
如图![]() ,连结PC,PB构成一个四棱锥
,连结PC,PB构成一个四棱锥![]() .
.

![]() Ⅰ
Ⅰ![]() 求证
求证![]() ;
;
![]() Ⅱ
Ⅱ![]() 若
若![]() 平面ABCD.
平面ABCD.
![]() 求二面角
求二面角![]() 的大小;
的大小;
![]() 在棱PC上存在点M,满足
在棱PC上存在点M,满足![]() ,使得直线AM与平面PBC所成的角为
,使得直线AM与平面PBC所成的角为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出定义:若![]() (其中
(其中![]() 为整数),则
为整数),则![]() 叫做离实数
叫做离实数![]() 最近的整数,记作
最近的整数,记作![]() ,即
,即![]() .设函数
.设函数![]() ,二次函数
,二次函数![]() ,若函数
,若函数![]() 与
与![]() 的图象有且只有一个公共点,则
的图象有且只有一个公共点,则![]() 的取值不可能是( )
的取值不可能是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题不正确的是( )
A.研究两个变量相关关系时,相关系数r为负数,说明两个变量线性负相关
B.研究两个变量相关关系时,相关指数R2越大,说明回归方程拟合效果越好.
C.命题“x∈R,cosx≤1”的否定命题为“x0∈R,cosx0>1”
D.实数a,b,a>b成立的一个充分不必要条件是a3>b3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:已知四棱锥P—ABCD的底面ABCD是平行四边形,PA⊥面ABCD,M是AD的中点,N是PC的中点.

(1)求证:MN∥面PAB;
(2)若平面PMC⊥面PAD,求证:CM⊥AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为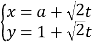 (
(![]() 为参数,
为参数, ![]() ),以
),以![]() 为极点,
为极点, ![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
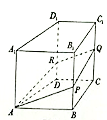
【题目】如图,在四棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 上一动点,过直线
上一动点,过直线![]() 的平面分别与棱
的平面分别与棱![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,则下列结论正确的是__________.
,则下列结论正确的是__________.
①对于任意的点![]() ,都有
,都有![]()
②对于任意的点![]() ,四边形
,四边形![]() 不可能为平行四边形
不可能为平行四边形
③存在点![]() ,使得
,使得![]() 为等腰直角三角形
为等腰直角三角形
④存在点![]() ,使得直线
,使得直线![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
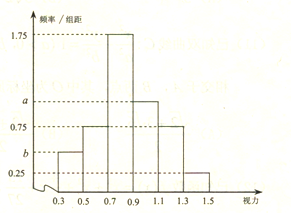
【题目】从某校高三年级中随机抽取100名学生,对其高校招生体检表中的视图情况进行统计,得到如图所示的频率分布直方图,已知从这100人中随机抽取1人,其视力在![]() 的概率为
的概率为![]() .
.
(1)求![]() 的值;
的值;
(2)若某大学![]() 专业的报考要求之一是视力在0.9以上,则对这100人中能报考
专业的报考要求之一是视力在0.9以上,则对这100人中能报考![]() 专业的学生采用按视力分层抽样的方法抽取8人,调查他们对
专业的学生采用按视力分层抽样的方法抽取8人,调查他们对![]() 专业的了解程度,现从这8人中随机抽取3人进行是否有意向报考该大学
专业的了解程度,现从这8人中随机抽取3人进行是否有意向报考该大学![]() 专业的调查,记抽到的学生中视力在
专业的调查,记抽到的学生中视力在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com