
【题目】如图所示,已知抛物线C:y2=4x的焦点为F,直线l经过点F且与抛物线C相交于A、B两点.

(1)若线段AB的中点在直线y=2上,求直线l的方程;
(2)若线段|AB|=20,求直线l的方程.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)设直线l的斜率为k,A(x1,y1),B(x2,y2),AB的中点M(x0,y0),由点差法,可得2y0k=4,又![]() ,所以
,所以![]() 。(2)设直线l的方程为x=my+1,与抛物线联立组方程组,由弦长公式与志达定理,可求得参数m的值.
。(2)设直线l的方程为x=my+1,与抛物线联立组方程组,由弦长公式与志达定理,可求得参数m的值.
试题解析:(1)由已知得抛物线的焦点为F(1,0).因为线段AB的中点在直线y=2上,所以直线l的斜率存在,设直线l的斜率为k,A(x1,y1),B(x2,y2),AB的中点M(x0,y0),
则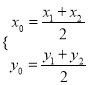 由
由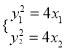 得
得
(y1+y2)(y1-y2)=4(x1-x2),所以2y0k=4.
又y0=2,所以k=1,故直线l的方程是y=x-1.
(2)设直线l的方程为x=my+1,与抛物线方程联立得![]() 消元得y2-4my-4=0,所以y1+y2=4m,y1y2=-4,Δ=16(m2+1)>0.
消元得y2-4my-4=0,所以y1+y2=4m,y1y2=-4,Δ=16(m2+1)>0.
|AB|=![]() |y1-y2|=
|y1-y2|=![]() ·
·![]()
=![]() ·
·![]() =4(m2+1).
=4(m2+1).
所以4(m2+1)=20,解得m=±2,
所以直线l的方程是x=±2y+1,
即x±2y-1=0.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}为等比数列, ![]() 公比为
公比为![]()
![]() 为数列{an}的前n项和.
为数列{an}的前n项和.
(1)若![]() 求
求![]() ;
;
(2)若调换![]() 的顺序后能构成一个等差数列,求
的顺序后能构成一个等差数列,求![]() 的所有可能值;
的所有可能值;
(3)是否存在正常数![]() ,使得对任意正整数n,不等式
,使得对任意正整数n,不等式![]() 总成立?若存在,求出
总成立?若存在,求出![]() 的范围,若不存在,请说明理由.
的范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知α,β是两个不同的平面,m,n分别是平面α与平面β之外的两条不同直线,给出四个论断:
①m⊥n;②α⊥β;③n⊥β;④m⊥α.
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:____.(用序号表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:曲线C:(m+2)x2+my2=1表示双曲线,命题q:方程y2=(m2﹣1)x表示的曲线是焦点在x轴的负半轴上的抛物线,若p∨q为真命题,p∧q为假命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥O﹣ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.

(1)求异面直线BE与AC所成角的余弦值;
(2)求直线BE和平面ABC的所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点。

(1)求直线AF与EC所成角的正弦值;
(2)求PE与平面PDB所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两名工人加工同一种零件,两人每天加工的零件数相同,所得次品数分别为![]() ,
,![]() ,
,![]() 和
和![]() 的分布列如下表.
的分布列如下表.

(![]() )分别求期望
)分别求期望![]() 和
和![]() .
.
(![]() )试对这两名工人的技术水平进行比较.
)试对这两名工人的技术水平进行比较.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2x的定义域是[2,16].设g(x)=f(2x)﹣[f(x)]2.
(1)求函数g(x)的解析式及定义域;
(2)求函数g(x)的最值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com