
【题目】已知函数f(x)=(a﹣bx3)ex﹣ ![]() ,且函数f(x)的图象在点(1,e)处的切线与直线x﹣(2e+1)y﹣3=0垂直.
,且函数f(x)的图象在点(1,e)处的切线与直线x﹣(2e+1)y﹣3=0垂直.
(Ⅰ)求a,b;
(Ⅱ)求证:当x∈(0,1)时,f(x)>2.
【答案】解:(Ⅰ)因为f(1)=e,故(a﹣b)e=e,故a﹣b=1①; 依题意,f′(1)=﹣2e﹣1;又 ![]() ,
,
故f′(1)=ae﹣1﹣4be=﹣2e﹣1,故a﹣4b=﹣2②,
联立①②解得a=2,b=1,
(Ⅱ)证明:由(Ⅰ)得 ![]()
要证f(x)>2,即证2ex﹣exx3>2+ ![]() ;
;
令g(x)=2ex﹣exx3 , ∴g′(x)=ex(﹣x3﹣3x2+2)=﹣ex(x3+3x2﹣2)=﹣ex(x+1)(x2+2x﹣2),
故当x∈(0,1)时,﹣ex<0,x+1>0;
令p(x)=x2+2x﹣2,因为p(x)的对称轴为x=﹣1,且p(0)p(1)<0,
故存在x0∈(0,1),使得p(x0)=0;
故当x∈(0,x0)时,p(x)=x2+2x﹣2<0,g′(x)=﹣ex(x+1)(x2+2x﹣2)>0,
即g(x)在(0,x0)上单调递增;
当x∈(x0 , 1)时,p(x)=x2+2x﹣2>0,故g′(x)=﹣ex(x+1)(x2+2x﹣2)<0,
即g(x)在(x0 , 1)上单调递减;因为g(0)=2,g(1)=e,
故当x∈(0,1)时,g(x)>g(0)=2,
又当x∈(0,1)时, ![]() ,∴
,∴ ![]()
所以2ex﹣exx3>2+ ![]() ,即f(x)>2
,即f(x)>2
【解析】(Ⅰ)根据函数f(x)的图象在点(1,e)处的切线与直线x﹣(2e+1)y﹣3=0垂直,求得a,b;(Ⅱ)由(Ⅰ)得 ![]() ,证f(x)>2,即证2ex﹣exx3>2+
,证f(x)>2,即证2ex﹣exx3>2+ ![]() ,构造函数,确定函数的单调性,即可证明结论.
,构造函数,确定函数的单调性,即可证明结论.
【考点精析】认真审题,首先需要了解函数的最大(小)值与导数(求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值).
比较,其中最大的是一个最大值,最小的是最小值).


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
【题目】中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美,给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”,给出下列命题:
①对于任意一个圆O,其“优美函数“有无数个”;
②函数 ![]() 可以是某个圆的“优美函数”;
可以是某个圆的“优美函数”;
③正弦函数y=sinx可以同时是无数个圆的“优美函数”;
④函数y=f(x)是“优美函数”的充要条件为函数y=f(x)的图象是中心对称图形.
其中正确的命题是( )
A.①③
B.①③④
C.②③
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题,其中正确的命题是____.(填出所有正确命题的序号)
①x=![]() 是y=sin(2x+
是y=sin(2x+![]() )的一条对称轴;
)的一条对称轴;
②y=esin2x是以π为周期在(0,![]() )上的增函数;
)上的增函数;
③函数y=3sin(2x+![]() )的图象可由y=3sin2x的图象向左平移
)的图象可由y=3sin2x的图象向左平移![]() 个单位得到.
个单位得到.
④设x1、x2是关于x的方程|logax|=k(a>0,a≠1,k>0)的两根,则x1x2=1;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解本校学生在校小卖部的月消费情况,随机抽取了60名学生进行统计.得到如下样本频数分布表:
月消费金额(单位:元) |
|
|
|
|
|
|
人数 | 30 | 6 | 9 | 10 | 3 | 2 |
记月消费金额不低于300元为“高消费”,已知在样本中随机抽取1人,抽到是男生“高消费”的概率为![]() .
.
(1)从月消费金额不低于400元的学生中随机抽取2人,求至少有1人月消费金额不低于500元的概率;
(2)请将下面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“高消费”与“男女性别”有关,说明理由.
的把握认为“高消费”与“男女性别”有关,说明理由.
高消费 | 非高消费 | 合计 | |
男生 | |||
女生 | 25 | ||
合计 | 60 |
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() ,其中)
,其中)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生的学习情况,某学校在一次考试中随机抽取了20名学生的成绩,分成[50,60),[60,70),[70,80),[80,90),[90,100]五组,绘制了如图所示频率分布直方图.求:

(Ⅰ)图中m的值;
(II)估计全年级本次考试的平均分;
(III)若从样本中随机抽取分数在[80,100]的学生两名,求所抽取两人至少有一人分数不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知符号函数sgnx= 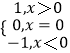 ,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),则( )
,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),则( )
A.sgn[g(x)]=sgnx
B.sgn[g(x)]=﹣sgnx
C.sgn[g(x)]=sgn[f(x)]
D.sgn[g(x)]=﹣sgn[f(x)]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com