
分析 (1)求导数,f′(x)=3ax2+x-2,根据x=-1是f(x)的极值点,便有f′(-1)=0,这样可求出a=1,而根据f(x)的图象过原点可得出c=0,这样即可得出f(x)=${x}^{3}+\frac{1}{2}{x}^{2}-2x$,从而求出f(-1)便是f(x)的极值;
(2)根据题意可知,g(-1)=$\frac{3}{2}$,这样可得到d=$\frac{1-b}{2}$,并且方程f(x)=g(x)有含x=-1的两个不同解,这样即可得到方程${x}^{3}+(\frac{1}{2}-\frac{1}{2}b){x}^{2}-x+\frac{b-1}{2}=0$,该方程可以设成$(x+1)({x}^{2}+ex+\frac{b-1}{2})=0$,这样便可以求出$e=-\frac{1+b}{2}$,从而得出方程${x}^{2}-\frac{1+b}{2}x+\frac{b-1}{2}=0$有两个相等的实数根,且不是-1,这样便有△=0,这样便可求出b的值,也就得到了b的取值范围.
解答 解:(1)f′(x)=3ax2+x-2;
x=-1是f(x)的极值点;
∴f′(-1)=3a-3=0;
∴a=1;
又f(x)的图象过原点;
∴c=0;
∴$f(x)={x}^{3}+\frac{1}{2}{x}^{2}-2x$;
∴f(x)的极值为f(-1)=$\frac{3}{2}$;
(2)根据题意,$g(-1)=\frac{1}{2}b+1+d=\frac{3}{2}$;
∴$d=\frac{1-b}{2}$;
令f(x)=g(x),即${x}^{3}+\frac{1}{2}{x}^{2}-2x=\frac{1}{2}b{x}^{2}-x+\frac{1-b}{2}$;
即${x}^{3}+(\frac{1}{2}-\frac{1}{2}b){x}^{2}-x+\frac{b-1}{2}=0$,该方程有两个不同的实数根,其中一个为-1;
∴该方程可设成$(x+1)({x}^{2}+ex+\frac{b-1}{2})=0$;
展开为:${x}^{3}+(1+e){x}^{2}+(e+\frac{b-1}{2})x+\frac{b-1}{2}=0$;
∴$1+e=\frac{1}{2}-\frac{1}{2}b$;
∴$e=-\frac{1+b}{2}$;
则方程${x}^{2}-\frac{1+b}{2}x+\frac{b-1}{2}=0$有2个相同的实根,且不为-1;
∴$△=(\frac{1+b}{2})^{2}-2(b-1)=0$,且1$+\frac{1+b}{2}+\frac{b-1}{2}≠0$;
解得b=3;
∴存在实数b,使得函数g(x)的图象与函数f(x)的图象恒有含x=-1的二个不同的交点,且实数b的取值范围为:{3}.
点评 考查函数极值点概念,函数在极值点处导数的取值情况,函数图象上点的坐标满足函数解析式,以及两函数图象的交点情况和两函数解析式形成的方程解的关系,一元二次方程的解的情况和判别式△取值的关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
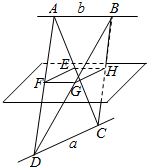 如图,平面EFGH分别平行于CD,AB,点E,F,G,H分别在AC,AD,BD,BC上,且CD=a,AB=b,CD⊥AB.
如图,平面EFGH分别平行于CD,AB,点E,F,G,H分别在AC,AD,BD,BC上,且CD=a,AB=b,CD⊥AB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com