
【题目】在锐角△ABC中,内角A,B,C所对的边分别为a,b,c,已知 ![]() a=2csinA.
a=2csinA.
(1)求角C的值;
(2)若c= ![]() ,且S△ABC=
,且S△ABC= ![]() ,求a+b的值.
,求a+b的值.
【答案】
(1)解:由 ![]() a=2csinA及正弦定理,得
a=2csinA及正弦定理,得 ![]() sinA=2sinCsinA,
sinA=2sinCsinA,
∵sinA≠0,
∴sinC= ![]() .
.
又∵△ABC是锐角三角形,
∴C= ![]()
(2)解:∵c= ![]() ,C=
,C= ![]() ,
,
∴由面积公式,得 ![]() absin
absin ![]() =
= ![]() ,即ab=6.①
,即ab=6.①
由余弦定理,得a2+b2﹣2abcos ![]() =7,
=7,
即a2+b2﹣ab=7.②
由②变形得(a+b)2=3ab+7.③
将①代入③得(a+b)2=25,故a+b=5
【解析】(1)由 ![]() a=2csinA及正弦定理得
a=2csinA及正弦定理得 ![]() sinA=2sinCsinA,又sinA≠0,可sinC=
sinA=2sinCsinA,又sinA≠0,可sinC= ![]() .又△ABC是锐角三角形,即可求C.(2)由面积公式,可解得ab=6,由余弦定理,可解得a2+b2﹣ab=7,联立方程即可解得a+b的值的值.
.又△ABC是锐角三角形,即可求C.(2)由面积公式,可解得ab=6,由余弦定理,可解得a2+b2﹣ab=7,联立方程即可解得a+b的值的值.
【考点精析】本题主要考查了正弦定理的定义的相关知识点,需要掌握正弦定理:![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A、B、C所对的边的长分别为a、b、c,设向量 ![]() =(a﹣c,a﹣b),
=(a﹣c,a﹣b), ![]() =(a+b,c),且
=(a+b,c),且 ![]() ∥
∥ ![]() ,
,
(1)求B;
(2)若a=1,b= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的图象过点P(0,2),且在点M(-1,
的图象过点P(0,2),且在点M(-1, ![]() )处的切线方程
)处的切线方程 ![]() 。
。
(1)求函数 ![]() 的解析式;
的解析式;
(2)求函数 ![]() 与
与 ![]() 的图像有三个交点,求a的取值范围。
的图像有三个交点,求a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,甲所得为( )
A.![]() 钱
钱
B.![]() 钱
钱
C.![]() 钱
钱
D.![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(其中 ![]() )的图象如图所示,为了得到g(x)=sin2x的图象,则只需将f(x)的图象( )
)的图象如图所示,为了得到g(x)=sin2x的图象,则只需将f(x)的图象( ) 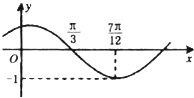
A.向右平移 ![]() 个长度单位
个长度单位
B.向右平移 ![]() 个长度单位
个长度单位
C.向左平移 ![]() 个长度单位
个长度单位
D.向左平移 ![]() 个长度单位
个长度单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=ax2﹣(a+1)x+1
(1)解关于x的不等式f(x)>0;
(2)若对任意的a∈[﹣1,1],不等式f(x)>0恒成立,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生对一些对数进行运算,如图表格所示:
x | 0.21 | 0.27 | 1.5 | 2.8 |
lgx | 2a+b+c﹣3(1) | 6a﹣3b﹣2(2) | 3a﹣b+c(3) | 1﹣2a+2b﹣c(4) |
x | 3 | 5 | 6 | 7 |
lgx | 2a﹣b(5) | a+c(6) | 1+a﹣b﹣c(7) | 2(a+c)(8) |
x | 8 | 9 | 14 | |
lgx | 3﹣3a﹣3c(9) | 4a﹣2b(10) | 1﹣a+2b(11) |
现在发觉学生计算中恰好有两次地方出错,那么出错的数据是( )
A.(3),(8)
B.(4),(11)
C.(1),(3)
D.(1),(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com