
【题目】已知椭圆C:![]() 的左焦点为
的左焦点为![]() ,且点
,且点![]() 在C上.
在C上.
![]() 求C的方程;
求C的方程;
![]() 设点P关于x轴的对称点为点
设点P关于x轴的对称点为点![]() 不经过P点且斜率为
不经过P点且斜率为![]() 的直线1与C交于A,B两点,直线PA,PB分别与x轴交于点M,N,求证:
的直线1与C交于A,B两点,直线PA,PB分别与x轴交于点M,N,求证:![]() .
.
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】已知甲箱中装有3个红球,2个黑球,乙箱中装有2个红球,3个黑球,这些球除颜色外完全相同,某商场举行有奖促销活动,规定顾客购物1000元以上,可以参与抽奖一次,设奖规则如下:每次分别从以上两个箱子中各随机摸出2个球,共4个球,若摸出4个球都是红球,则获得一等奖,奖金300元;摸出的球中有3个红球,则获得二等奖,奖金200元;摸出的球中有2个红球,则获得三等奖,奖金100元;其他情况不获奖,每次摸球结束后将球放回原箱中.
(1)求在1次摸奖中,获得二等奖的概率;
(2)若3人各参与摸奖1次,求获奖人数X的数学期望![]() ;
;
(3)若商场同时还举行打9折促销活动,顾客只能在两项促销活动中任选一项参与.假若你购买了价值1200元的商品,那么你选择参与哪一项活动对你有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋里装有大小相同的5个小球,其中红色两个,其余3个颜色各不相同![]() 现从中任意取出3个小球,其中恰有2个小球颜色相同的概率是______;若变量X为取出的三个小球中红球的个数,则X的数学期望
现从中任意取出3个小球,其中恰有2个小球颜色相同的概率是______;若变量X为取出的三个小球中红球的个数,则X的数学期望![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有报道称,据南方科技大学、上海交大等8家单位的最新研究显示:A、B、O、AB血型与COVID﹣19易感性存在关联,具体调查数据统计如图:

根据以上调查数据,则下列说法错误的是( )
A.与非O型血相比,O型血人群对COVID﹣19相对不易感,风险较低
B.与非A型血相比,A型血人群对COVID﹣19相对易感,风险较高
C.与O型血相比,B型、AB型血人群对COVID﹣19的易感性要高
D.与A型血相比,非A型血人群对COVID﹣19都不易感,没有风险
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形.谢尔宾斯基三角形是一种分形,由波兰数学家谢尔宾斯基1915年提出.具体操作是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形,如上图.现在图(3)中随机选取一个点,则此点取自阴影部分的概率为________

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 离心率为
离心率为![]() ,以原点为圆心,以椭圆C的短半轴长为半径的圆O与直线
,以原点为圆心,以椭圆C的短半轴长为半径的圆O与直线![]() :
:![]() 相切.
相切.
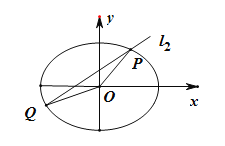
(1)求椭圆C的方程;
(2)设不过原点O的直线![]() 与该椭圆交于P、Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.
与该椭圆交于P、Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察下列事实:|x|+|y|≤1的不同整数解(x,y)的个数为5,|x|+|y|≤2的不同整数解(x,y)的个数为13,|x|+|y|≤3的不同整数解(x,y)的个数为25,|x|+|y|≤4的不同整数解(x,y)的个数为41,|x|+|y|≤5的不同整数解(x,y)的个数为61,….则|x|+|y|≤20的不同整数解(x,y)的个数为( )
A.841B.761C.925D.941
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com