
【题目】在一个不透明的箱子里装有5个完全相同的小球,球上分别标有数字1、2、3、4、5.甲先从箱子中摸出一个小球,记下球上所标数字后,将该小球放回箱子中摇匀后,乙再从该箱子中摸出一个小球.
(1)若甲、乙两人谁摸出的球上标的数字大谁就获胜(数字相同为平局),求甲获胜的概率;
(2)规定:两人摸到的球上所标数字之和小于6,则甲获胜,否则乙获胜,这样规定公平吗?
【答案】(1)![]() (2)不公平
(2)不公平
【解析】用(x,y)(x表示甲摸到的数字,y表示乙摸到的数字)表示甲、乙各摸一球构成基本事件,则基本事件为(1,1),(1,2)、(1,3)、(1,4)、(1,5)、(2,1)、(2,2)、(2,3)、(2,4)、(2、5)、(3,1)、(3,2)、(3,3)、(3,4)、(3、5)、(4,1)、(4,2)、(4,3)、(4,4)、(4,5)、(5,1)、(5,2)、(5,3)、(5,4)、(5,5),共25个.
(1)设甲获胜为事件A,则事件A包含的基本事件有(2,1)、(3,1)、(3,2)(4,1)、(4,2)、(4,3)、(5,1)、(5,2)、(5,3)、(5,4),共有10个,则甲获胜的概率为![]()
(2)设甲获胜的事件为B,乙获胜的事件为C.事件B所包含的基本事件有(1,1),(1,2)、(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2),(4,1),共有10个,则![]() ,所以
,所以![]() .
.
因为![]() ,所以这样规定不公平.
,所以这样规定不公平.


科目:高中数学 来源: 题型:
【题目】已知矩阵![]() 将直线l:x+y-1=0变换成直线l′.
将直线l:x+y-1=0变换成直线l′.
(1)求直线l′的方程;
(2)判断矩阵A是否可逆?若可逆,求出矩阵A的逆矩阵A-1;若不可逆,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥曲线![]() :
:  (
(![]() 为参数)和定点
为参数)和定点![]() ,
, ![]() ,
, ![]() 是此圆锥曲线
是此圆锥曲线![]() 的左、右焦点.
的左、右焦点.
(1)以原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,求直线
轴的正半轴为极轴建立极坐标系,求直线![]() 的极坐标方程;
的极坐标方程;
(2)经过![]() 且与直线
且与直线![]() 垂直的直线交此圆锥曲线
垂直的直线交此圆锥曲线![]() 于
于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器由于使用时间较长,生产的零件有一些缺损,按不同转速生产出来的零件有缺损的统计数据如下表所示.
(1)作出散点图;
(2)如果y与x线性相关,求出回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么机器的运转速度应控制在什么范围内?
转速x(转/秒) | 16 | 14 | 12 | 8 |
每小时生产有缺损零件数y(个) | 11 | 9 | 8 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有除颜色外其余均相同的12个小球,从中随机取出1个球,取出红球的概率为![]() ,取出黑球的概率为
,取出黑球的概率为![]() ,取出白球的概率为
,取出白球的概率为![]() ,取出绿球的概率为
,取出绿球的概率为![]() .求:
.求:
(1)取出的1个球是红球或黑球的概率;
(2)取出的1个球是红球或黑球或白球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,底面是等腰直角三角形,
中,底面是等腰直角三角形, ![]() ,侧棱
,侧棱![]() ,点
,点![]() 分别为棱
分别为棱![]() 的中点,
的中点, ![]() 的重心为
的重心为![]() ,直线
,直线![]() 垂直于平面
垂直于平面![]() .
.
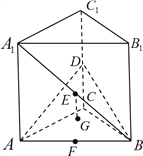
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦.
的余弦.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]()
![]() 的上焦点为
的上焦点为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点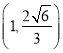 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设过椭圆![]() 的上顶点
的上顶点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com