
【题目】已知函数![]() ,
, ![]() ,
, ![]() 为实数,
为实数, ![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() .
.
(1)当![]() ,
, ![]() 时,设函数
时,设函数![]() 的最小值为
的最小值为![]() ,求
,求![]() 的最大值;
的最大值;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不同实数解,求
上有两个不同实数解,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)先求函数导数,并在定义域内求导函数零点: ![]() ,再列表分析导函数符号变化规律,确定单调性及最小值
,再列表分析导函数符号变化规律,确定单调性及最小值
![]()
![]() ,再利用导数研究函数
,再利用导数研究函数![]() 最值:先求导数,确定定义域内导函数零点,最后根据单调性确定函数最值.(2)先变量分离:
最值:先求导数,确定定义域内导函数零点,最后根据单调性确定函数最值.(2)先变量分离: ![]() ,转化为研究函数
,转化为研究函数![]() 图像:当
图像:当![]() 时,
时, ![]() 单调减,
单调减, ![]() ;当
;当![]() 时,
时, ![]() 单调增,
单调增, ![]() , 因此有两个不同实数解需
, 因此有两个不同实数解需![]() ,
,
试题解析:解:(1)当![]() 时,函数
时,函数![]() ,
,
则![]()
![]() ,
,
令![]() ,得
,得![]() ,因为
,因为![]() 时,
时, ![]() ,
,

所以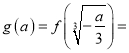
![]()
![]() ,
,
令![]() ,
,
则![]() ,令
,令![]() ,得
,得![]() ,
,
且当![]() 时,
时, ![]() 有最大值1,
有最大值1,
所以![]() 的最大值为1(表格略),(分段写单调性即可),此时
的最大值为1(表格略),(分段写单调性即可),此时![]() .
.
(2)由题意得,方程![]() 在区间
在区间![]() 上有两个不同实数解,
上有两个不同实数解,
所以![]() 在区间
在区间![]() 上有两个不同的实数解,
上有两个不同的实数解,
即函数![]() 图象与函数
图象与函数![]() 图象有两个不同的交点,
图象有两个不同的交点,
因为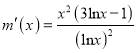 ,令
,令![]() ,得
,得![]() ,
,
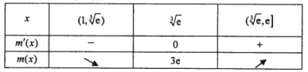
所以当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
,
所以![]() ,
, ![]() 满足的关系式为
满足的关系式为![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】统计表明,某种型号的汽车在匀速行驶中每小时耗油量![]() (升)关于行驶速度
(升)关于行驶速度![]() (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: ![]() ,已知甲、乙两地相距100千米.
,已知甲、乙两地相距100千米.
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一袋中装有6个黑球,4个白球.如果不放回地依次取出2个球.求:
(1)第1次取到黑球的概率;
(2)第1次和第2次都取到黑球的概率;
(3)在第1次取到黑球的条件下,第2次又取到黑球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn,已知a1=10,a2为整数,且Sn≤S4.
(1)求{an}的通项公式;
(2)设bn=![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 为非零常数.
为非零常数.
(1)若![]() ,
, ![]() ,求证:
,求证: ![]() 为等比数列,并求数列
为等比数列,并求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 是公差不等于零的等差数列.
是公差不等于零的等差数列.
①求实数![]() ,
, ![]() 的值;
的值;
②数列![]() 的前
的前![]() 项和
项和![]() 构成数列
构成数列![]() ,从
,从![]() 中取不同的四项按从小到大排列组成四项子数列.试问:是否存在首项为
中取不同的四项按从小到大排列组成四项子数列.试问:是否存在首项为![]() 的四项子数列,使得该子数列中的所有项之和恰好为2017?若存在,求出所有满足条件的四项子数列;若不存在,请说明理由.
的四项子数列,使得该子数列中的所有项之和恰好为2017?若存在,求出所有满足条件的四项子数列;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(sinx,sin(x﹣
=(sinx,sin(x﹣ ![]() )),
)), ![]() =(sinx,cos(x+
=(sinx,cos(x+ ![]() )),f(x)=
)),f(x)= ![]()
![]() .
.
(1)求f(x)的解析式及周期;
(2)求f(x)在x∈[﹣ ![]() ,
, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双“十一”结束之后,某网站针对购物情况进行了调查,参与调查的人主要集中在[20,50]岁之间,若规定:购物600(含600元)以下者,称为“理智购物”,购物超过600元者被网友形象的称为“剁手党”,得到如下统计表:
分组编号 | 年龄分组 | 球迷 | 所占比例 |
1 | [20,25) | 1000 | 0.5 |
2 | [25,30) | 1800 | 0.6 |
3 | [30,35) | 1200 | 0.5 |
4 | [35,40) | a | 0.4 |
5 | [40,45) | 300 | 0.2 |
6 | [45,50] | 200 | 0.1 |
若参与调查的“理智购物”总人数为7720人.
(1)求a的值;
(2)从年龄在[20,35)的“剁手党”中按照年龄区间分层抽样的方法抽取20人; ①从这20人中随机抽取2人,求这2人恰好属于同一年龄区间的概率;
②从这20人中随机抽取2人,用ζ表示年龄在[20,25)之间的人数,求ξ的分布列及期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x(lnx﹣ax).
(1)a= ![]() 时,求f(x)在点(1,f(1))处的切线方程;
时,求f(x)在点(1,f(1))处的切线方程;
(2)若f(x)存在两个不同的极值x1 , x2 , 求a的取值范围;
(3)在(2)的条件下,求f(x)在(0,a]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣x
(1)求f(x)的解析式;
(2)画出f(x)的图象;
(3)若方程f(x)=k有4个解,求k的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com