
【题目】已知f(x)是定义在(﹣1,1)上的偶函数,当x∈[0,1)时f(x)=lg ![]() ,
,
(1)求f(x)的解析式;
(2)探求f(x)的单调区间,并证明f(x)的单调性.
【答案】
(1)解:设x∈(﹣1,0),则﹣x∈(0,1),
∴f(﹣x)=lg ![]() ,
,
∵f(x)是定义在(﹣1,1)上的偶函数,
∴f(x)=f(﹣x)=lg ![]() ,
,
综上可得:f(x)= 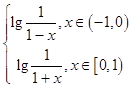
(2)解:f(x)在[0,1)上单调递减,在(﹣1,0)单调递增.证明如下:
∵f′(x)= 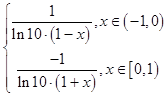 ,
,
当x∈(﹣1,0)时,f′(x)>0恒成立,
当x∈[0,1),f′(x)<0恒成立,
故f(x)在[0,1)上单调递减,在(﹣1,0)单调递增
【解析】(1)根据f(x)是定义在(﹣1,1)上的偶函数,当x∈[0,1)时f(x)=lg ![]() ,求出x∈(﹣1,0)时函数的解析式,综合可得答案;(2)f(x)在[0,1)上单调递减,在(﹣1,0)单调递增,利用导数法可证得结论.
,求出x∈(﹣1,0)时函数的解析式,综合可得答案;(2)f(x)在[0,1)上单调递减,在(﹣1,0)单调递增,利用导数法可证得结论.
【考点精析】本题主要考查了奇偶性与单调性的综合和利用导数研究函数的单调性的相关知识点,需要掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的左右焦点F1、F2 , 离心率为
=1(a>b>0)的左右焦点F1、F2 , 离心率为 ![]() ,双曲线方程为
,双曲线方程为 ![]() =1(a>0,b>0),直线x=2与双曲线的交点为A、B,且|AB|=
=1(a>0,b>0),直线x=2与双曲线的交点为A、B,且|AB|= ![]() .
.
(Ⅰ)求椭圆与双曲线的方程;
(Ⅱ)过点F2的直线l与椭圆交于M、N两点,交双曲线与P、Q两点,当△F1MN(F1为椭圆的左焦点)的内切圆的面积取最大值时,求△F1PQ的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,圆
,圆![]() ,点
,点![]() 为抛物线
为抛物线![]() 上的动点,
上的动点, ![]() 为坐标原点,线段
为坐标原点,线段![]() 的中点
的中点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)点![]() 是曲线
是曲线![]() 上的点,过点
上的点,过点![]() 作圆
作圆![]() 的两条切线,分别与
的两条切线,分别与![]() 轴交于
轴交于![]() 两点.
两点.
求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若Sn=cos ![]() +cos
+cos ![]() +…+cos
+…+cos ![]() (n∈N+),则在S1 , S2 , …,S2015中,正数的个数是( )
(n∈N+),则在S1 , S2 , …,S2015中,正数的个数是( )
A.882
B.756
C.750
D.378
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1中,∠BCA=90°,M,N分别是A1B1 , A1C1的中点,BC=CA=CC1 , 则BM与AN所成角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD= ![]() .
.
(Ⅰ)求证:PD⊥平面PAB;
(Ⅱ)求直线PB与平面PCD所成角的正弦值;
(Ⅲ)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求 ![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.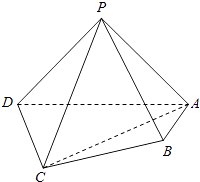
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com