
【题目】已知函数f(x)=x2+(lga+2)x+lgb满足f(﹣1)=﹣2且对于任意x∈R,恒有f(x)≥2x成立.
(1)求实数a,b的值;
(2)解不等式f(x)<x+5.
【答案】(1)100;(2)![]()
【解析】试题分析:(1)由![]() ,代入函数解析式得到化简后得到关于
,代入函数解析式得到化简后得到关于![]() 的等式记作②,又因为
的等式记作②,又因为![]() 恒成立,把
恒成立,把![]() 的解析式代入后,令
的解析式代入后,令![]() 0,根据平方大于等于0,即可求出
0,根据平方大于等于0,即可求出![]() 的值,把
的值,把![]() 的值代入②即可求出
的值代入②即可求出![]() 的值;
的值;
(2)由(1)可确定出![]() 的解析式,然后解关于
的解析式,然后解关于![]() 的一元二次不等式即可.
的一元二次不等式即可.
试题解析:(1)由f(﹣1)=﹣2知,lgb﹣lga+1=0①,所以![]() ②.
②.
又f(x)≥2x恒成立,f(x)﹣2x≥0恒成立,
则有x2+xlga+lgb≥0恒成立,
故△=(lga)2﹣4lgb≤0,
将①式代入上式得:(lgb)2﹣2lgb+1≤0,即(lgb﹣1)2≤0,
故lgb=1即b=10,代入②得,a=100;
(2)由(1)知f(x)=x2+4x+1,f(x)<x+5,
即x2+4x+1<x+5,
所以x2+3x﹣4<0,
解得﹣4<x<1,
因此不等式的解集为{x|﹣4<x<1}.


科目:高中数学 来源: 题型:
【题目】某居民区的物业部门每月向居民收取卫生费,计费方法如下:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.设计一个算法,根据输入的人数,计算应收取的卫生费,并画出程序框图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形.

(1)在图中画出这个正方形(不必说明画法和理由);
(2)求直线AF与平面α所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P为椭圆C: ![]() =1(a>b>0)的下顶点,M,N在椭圆上,若四边形OPMN为平行四边形,α为直线ON的倾斜角,若α∈(
=1(a>b>0)的下顶点,M,N在椭圆上,若四边形OPMN为平行四边形,α为直线ON的倾斜角,若α∈( ![]() ,
, ![]() ],则椭圆C的离心率的取值范围为( )
],则椭圆C的离心率的取值范围为( )
A.(0, ![]() ]
]
B.(0, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:函数f(x)= ![]() (a>0且a≠1).
(a>0且a≠1).
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)判断函数f(x)的奇偶性,并加以证明;
(Ⅲ)设a=![]() ,解不等式f(x)>0.
,解不等式f(x)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mlnx﹣x2+2(m∈R).
(1)当m=1时,求f(x)的单调区间;
(2)若f(x)在x=1时取得极大值,求证:f(x)﹣f′(x)≤4x﹣3;
(3)若m≤8,当x≥1时,恒有f(x)﹣f′(x)≤4x﹣3恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
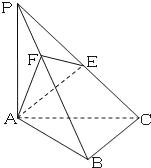
【题目】已知在三棱锥P﹣ABC中,PA⊥面ABC,AC⊥BC,且PA=AC=BC=1,点E是PC的中点,作EF⊥PB交PB于点F.
(Ⅰ)求证:PB⊥平面AEF;
(Ⅱ)求二面角A﹣PB﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 是函数f(x)=msinωx﹣cosωx(m>0)的一条对称轴,且f(x)的最小正周期为π
是函数f(x)=msinωx﹣cosωx(m>0)的一条对称轴,且f(x)的最小正周期为π
(Ⅰ)求m值和f(x)的单调递增区间;
(Ⅱ)设角A,B,C为△ABC的三个内角,对应边分别为a,b,c,若f(B)=2, ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com