
【题目】如图,在南北方向有一条公路,一半径为100![]() 的圆形广场(圆心为
的圆形广场(圆心为![]() )与此公路所在直线
)与此公路所在直线![]() 相切于点
相切于点![]() ,点
,点![]() 为北半圆弧(弧
为北半圆弧(弧![]() )上的一点,过点
)上的一点,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,计划在
,计划在![]() 内(图中阴影部分)进行绿化,设
内(图中阴影部分)进行绿化,设![]() 的面积为
的面积为![]() (单位:
(单位:![]() ),
),

(1)设![]() ,将
,将![]() 表示为
表示为![]() 的函数;
的函数;
(2)确定点![]() 的位置,使绿化面积最大,并求出最大面积.
的位置,使绿化面积最大,并求出最大面积.
科目:高中数学 来源: 题型:
【题目】某个地区计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水的年入流量![]() (年入流量:一年内上游来水与库区降水之和,单位:十亿立方米)都在4以上,其中,不足8的年份有10年,不低于8且不超过12的年份有35年,超过12的年份有5年,将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和,单位:十亿立方米)都在4以上,其中,不足8的年份有10年,不低于8且不超过12的年份有35年,超过12的年份有5年,将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多有1年的年入流量超过12的概率;
(2)若水的年入流量![]() 与其蕴含的能量
与其蕴含的能量![]() (单位:百亿万焦)之间的部分对应数据为如下表所示:
(单位:百亿万焦)之间的部分对应数据为如下表所示:
年入流量 | 6 | 8 | 10 | 12 | 14 |
蕴含的能量 | 1.5 | 2.5 | 3.5 | 5 | 7.5 |
用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;(回归方程系数用分数表示)
;(回归方程系数用分数表示)
(3)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
附:回归方程系数公式: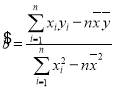 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个湖的边界是圆心为O的圆,湖的一侧有一条直线型公路l,湖上有桥AB(AB是圆O的直径).规划在公路l上选两个点P、Q,并修建两段直线型道路PB、QA.规划要求:线段PB、QA上的所有点到点O的距离均不小于圆O的半径.已知点A、B到直线l的距离分别为AC和BD(C、D为垂足),测得AB=10,AC=6,BD=12(单位:百米).
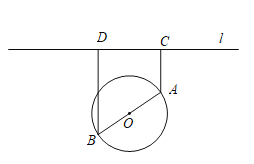
(1)若道路PB与桥AB垂直,求道路PB的长;
(2)在规划要求下,P和Q中能否有一个点选在D处?并说明理由;
(3)对规划要求下,若道路PB和QA的长度均为d(单位:百米).求当d最小时,P、Q两点间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某城市小区有一个矩形休闲广场,![]() 米,广场的一角是半径为
米,广场的一角是半径为![]() 米的扇形
米的扇形![]() 绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅
绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅![]() (宽度不计),点
(宽度不计),点![]() 在线段
在线段![]() 上,并且与曲线
上,并且与曲线![]() 相切;另一排为单人弧形椅沿曲线
相切;另一排为单人弧形椅沿曲线![]() (宽度不计)摆放.已知双人靠背直排椅的造价每米为
(宽度不计)摆放.已知双人靠背直排椅的造价每米为![]() 元,单人弧形椅的造价每米为
元,单人弧形椅的造价每米为![]() 元,记锐角
元,记锐角![]() ,总造价为
,总造价为![]() 元.
元.
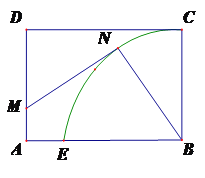
(1)试将![]() 表示为
表示为![]() 的函数
的函数![]() ,并写出
,并写出![]() 的取值范围;
的取值范围;
(2)如何选取点![]() 的位置,能使总造价
的位置,能使总造价![]() 最小.
最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块半圆形空地,开发商计划建造一个矩形游泳池![]() 及左右两侧两个大小相同的矩形休息区,其中半圆的圆心为
及左右两侧两个大小相同的矩形休息区,其中半圆的圆心为![]() ,半径为
,半径为![]() ,矩形
,矩形![]() 的一边
的一边![]() 在
在![]() 上,矩形
上,矩形![]() 的一边
的一边![]() 在
在![]() 上,点
上,点![]() 在圆周上,
在圆周上,![]() 在直径上,且
在直径上,且![]() ,设
,设![]() .若每平方米游泳池的造价和休息区造价分别为
.若每平方米游泳池的造价和休息区造价分别为![]() 和
和![]() .
.
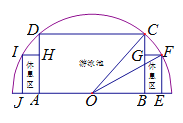
(1)记游泳池及休息区的总造价为![]() ,求
,求![]() 的表达式;
的表达式;
(2)为进行投资预算,当![]() 为何值时,总造价最大?并求出总造价的最大值.
为何值时,总造价最大?并求出总造价的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的产品中分正品与次品,正品重![]() ,次品重
,次品重![]() ,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第
,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第![]() 袋取出
袋取出![]() 个产品(
个产品(![]() ),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量
),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量![]() ,若次品所在的袋子的编号是2,此时的重量
,若次品所在的袋子的编号是2,此时的重量![]() _________
_________![]() ;若次品所在的袋子的编号是
;若次品所在的袋子的编号是![]() ,此时的重量
,此时的重量![]() _______
_______![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com