
【题目】为筛查在人群中传染的某种病毒,现有两种检测方法:
(1)抗体检测法:每个个体独立检测,每一次检测成本为80元,每个个体收取检测费为100元.
(2)核酸检测法:先合并个体,其操作方法是:当个体不超过10个时,把所有个体合并在一起进行检测.
当个体超过10个时,每10个个体为一组进行检测.若该组检测结果为阴性(正常),则只需检测一次;若该组检测结果为阳性(不正常),则需再对每个个体按核酸检测法重新独立检测,共需检测k+1次(k为该组个体数,1≤k≤10,k∈N*).每一次检测成本为160元.假设在接受检测的个体中,每个个体的检测结果是阳性还是阴性相互独立,且每个个体是阳性结果的概率均为p(0<p<1).
(Ⅰ)现有100个个体采取抗体检测法,求其中恰有一个检测出为阳性的概率;
(Ⅱ)因大多数人群筛查出现阳性的概率很低,且政府就核酸检测法给子检测机构一定的补贴,故检测机构推出组团选择核酸检测优惠政策如下:无论是检测一次还是k+1次,每组所有个体共收费700元(少于10个个体的组收费金额不变).已知某企业现有员工107人,准备进行全员检测,拟准备9000元检测费,由于时间和设备条件的限制,采用核酸检测法合并个体的组数不得高于参加采用抗体检测法人数,请设计一个合理的的检测安排方案;
(Ⅲ)设![]() ,现有n(n∈N*且2≤n≤10)个个体,若出于成本考虑,仅采用一种检测方法,试问检测机构应采用哪种检测方法?(ln3≈1.099,ln4≈1.386,ln5≈1.609,ln6≈1.792)
,现有n(n∈N*且2≤n≤10)个个体,若出于成本考虑,仅采用一种检测方法,试问检测机构应采用哪种检测方法?(ln3≈1.099,ln4≈1.386,ln5≈1.609,ln6≈1.792)
【答案】(Ⅰ)![]() .(Ⅱ)见解析(Ⅲ)当n=2时,采用抗体检测法,当3≤n≤10,n∈N*时,采用核酸检测法.
.(Ⅱ)见解析(Ⅲ)当n=2时,采用抗体检测法,当3≤n≤10,n∈N*时,采用核酸检测法.
【解析】
(Ⅰ)利用n次独立重复试验中事件A恰好发生k次概率计算公式能求出其中恰有一个检测出为阳性的概率;(Ⅱ)设安排x个个体采用抗体检测法,y组个体采用核酸检测法,根据已知条件列出不等式组,总检测费用为z=100x+700y,利用线性规划设计合理的安排方案;(Ⅲ)分别求出两种检测法的成本期望,由EX>EY推导出ln(![]() )
)![]() ,利用导数研究函数
,利用导数研究函数![]() 的单调性从而求出n的取值范围,即可确定检测方法.
的单调性从而求出n的取值范围,即可确定检测方法.
(Ⅰ)现有100个个体采取抗体检测法,其中恰有一个检测出为阳性的概率为:
P![]() .
.
(Ⅱ)设安排x个个体采用抗体检测法,y组个体采用核酸检测法,
则由条件知: ,x,y∈N,
,x,y∈N,
总检测费用为![]() .
.
画出可行域如图,
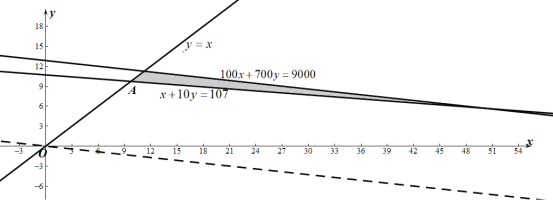
由![]() ,解得A(
,解得A(![]() ,
,![]() ),
),
则在可行域内临近A点的整点有(10,10),(17,9),此时,Zmin=8000,
即安排17人采取抗体检测法,90人采用核酸检测法,或者安排10人采取抗体检测法,97人采用核酸检测法,可使所有员工参加检测,且费用偏低.
(Ⅲ)设采用抗体检测法,检测机构成本期望为EX,则![]() ,
,
采用核酸检测,检测机构成本期望为EY,
设采用核酸检测法检测次数为η,则η的取值只有1和n+1,
且![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
设EX>EY,则![]() ,即
,即![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]()
![]() ,
,
设![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() ,
,![]() ,得
,得![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
又![]()
![]() ,
,
![]() ,
,
∴当n≥3,![]() 时,EX>EY,
时,EX>EY,
∴当n=2时,采用抗体检测法,当3≤n≤10,![]() 时,采用核酸检测法.
时,采用核酸检测法.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形ABCD是矩形,平面
中,四边形ABCD是矩形,平面![]() 平面ABCD,
平面ABCD,![]() ,E是SB的中点,M是CD上任意一点.
,E是SB的中点,M是CD上任意一点.
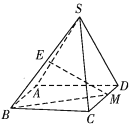
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 平面SAD,求直线BM与平面SAB所成角的正弦值.
平面SAD,求直线BM与平面SAB所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲,乙两种不透明充气包装的袋装零食,每袋零食甲随机附赠玩具![]() ,
,![]() ,
,![]() 中的一个,每袋零食乙从玩具
中的一个,每袋零食乙从玩具![]() ,
,![]() 中随机附赠一个.记事件
中随机附赠一个.记事件![]() :一次性购买
:一次性购买![]() 袋零食甲后集齐玩具
袋零食甲后集齐玩具![]() ,
,![]() ,
,![]() ;事件
;事件![]() :一次性购买
:一次性购买![]() 袋零食乙后集齐玩具
袋零食乙后集齐玩具![]() ,
,![]() .
.
(1)求概率![]() ,
,![]() 及
及![]() ;
;
(2)已知![]() ,其中
,其中![]() ,
,![]() 为常数,求
为常数,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AB⊥侧面BCC1B1,AC=AB1.
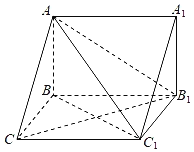
(1)求证:平面ABC1⊥平面AB1C;
(2)若AB=BC=2,∠BCC1=60°,求二面角B﹣AC1﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱锥S一ABC中,△ABC与△SBC都是边长为1的正三角形,二面角A﹣BC﹣S的大小为![]() ,若S,A,B,C四点都在球O的表面上,则球O的表面积为( )
,若S,A,B,C四点都在球O的表面上,则球O的表面积为( )
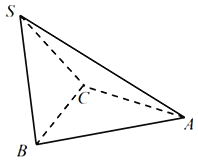
A.![]() πB.
πB.![]() πC.
πC.![]() πD.3π
πD.3π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为正项数列
为正项数列![]() 的前
的前![]() 项和,满足
项和,满足![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)若不等式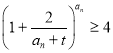 对任意正整数
对任意正整数![]() 都成立,求实数
都成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]() (其中
(其中![]() 是自然对数的底数),求证:
是自然对数的底数),求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com