
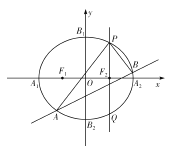
【题目】如图,已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,上、下顶点分别为
,上、下顶点分别为![]() ,两个焦点分别为
,两个焦点分别为![]() ,
, ![]() ,四边形
,四边形![]() 的面积是四边形
的面积是四边形![]() 的面积的2倍.
的面积的2倍.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右焦点且垂直于
的右焦点且垂直于![]() 轴的直线交椭圆
轴的直线交椭圆![]() 于
于![]() 两点,
两点, ![]() 是椭圆
是椭圆![]() 上位于直线
上位于直线![]() 两侧的两点.若
两侧的两点.若![]() ,求证:直线
,求证:直线![]() 的斜率
的斜率![]() 为定值.
为定值.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】试题分析:(1) 因为![]() ,所以
,所以![]() ,①由四边形
,①由四边形![]() 的面积是四边形
的面积是四边形![]() 的面积的2倍,可得
的面积的2倍,可得![]() .② 联立 ①② 解出a,b,c(2)由(1)易知点
.② 联立 ①② 解出a,b,c(2)由(1)易知点![]() 的坐标分別为
的坐标分別为![]() 若
若![]() ,所以直线
,所以直线![]() 的斜率之和为0. 设直线
的斜率之和为0. 设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() ,
, ![]() ,
,
直线![]() 的方程为
的方程为![]() ,由
,由 可得
可得![]() ,∴
,∴![]() ,同理直线
,同理直线![]() 的方程为
的方程为![]() ,
,
可得![]() ,∴
,∴![]() ,
,
![]()
![]() 把上边式子代入即得解.
把上边式子代入即得解.
试题解析:
(1)因为![]() ,所以
,所以![]() ,①
,①
由四边形![]() 的面积是四边形
的面积是四边形![]() 的面积的2倍,
的面积的2倍,
可得![]() .②
.②
由①可得![]() ,所以
,所以![]() ,所以
,所以![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)由(1)易知点![]() 的坐标分別为
的坐标分別为![]() 若
若![]() ,所以直线
,所以直线![]() 的斜率之和为0.
的斜率之和为0.
设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() ,
, ![]() ,
,
直线![]() 的方程为
的方程为![]() ,由
,由
可得![]() ,∴
,∴![]() ,
,
同理直线![]() 的方程为
的方程为![]() ,
,
可得![]() ,∴
,∴![]() ,
,
![]()
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,满足:a2+c2=b2+ ![]() ac
ac
(1)求∠B 的大小;
(2)求 ![]() cosA+cosC 的最大值.
cosA+cosC 的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x﹣1,f2(x)=x3 , f3(x)=x,f4(x)=log2(x+1),有以下结论: ①当x>1时,甲走在最前面;
②当x>1时,乙走在最前面;
③当0<x<1时,丁走在最前面,当x>1时,丁走在最前面;
④丙不可能走在最前面,也不可能走在最后面;
⑤如果它们一直运动下去,最终走在最前面的是甲.
其中,正确结论的序号为(把正确结论的序号都填上,多填或少填均不得分)
查看答案和解析>>
科目:高中数学 来源: 题型:
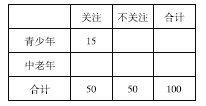
【题目】2016年6月22 日,“国际教育信息化大会”在山东青岛开幕.为了解哪些人更关注“国际教育信息化大会”,某机构随机抽取了年龄在15-75岁之间的100人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为: ![]() .把年龄落在区间
.把年龄落在区间![]() 和
和![]() 内的人分别称为 “青少年”和“中老年”.
内的人分别称为 “青少年”和“中老年”.
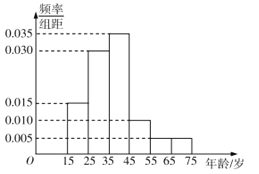
(1)根据频率分布直方图求样本的中位数(保留两位小数)和众数;
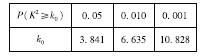
(2)根据已知条件完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”;
的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”;
附:参考公式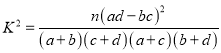 ,其中
,其中![]() .
.
临界值表:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆心坐标为( ![]() ,1)的圆M与x轴及直线y=
,1)的圆M与x轴及直线y= ![]() x分别相切于A,B两点,另一圆N与圆M外切、且与x轴及直线y=
x分别相切于A,B两点,另一圆N与圆M外切、且与x轴及直线y= ![]() x分别相切于C、D两点.
x分别相切于C、D两点. 
(1)求圆M和圆N的方程;
(2)过点B作直线MN的平行线l,求直线l被圆N截得的弦的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市对创“市级优质学校”的甲、乙两所学校复查验收,对办学的社会满意度一项评价随机访问了![]() 位市民,根据这
位市民,根据这![]() 位市民对这两所学校的评分(评分越高表明市民的评价越好),绘制茎叶图如下:
位市民对这两所学校的评分(评分越高表明市民的评价越好),绘制茎叶图如下:
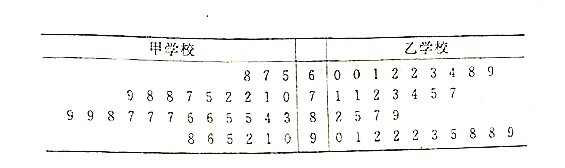
(1)分别估计该市的市民对甲、乙两所学校评分的中位数;
(2)分别估计该市的市民对甲、乙两所学校的评分不低于![]() 分的概率;
分的概率;
(3)根据茎叶图分析该市的市民对甲、乙两所学校的评价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com