
【题目】已知数列{an}的前n项和为Sn , 若4Sn=(2n﹣1)an+1+1,且a1=1.
(1)求数列{an}的通项公式;
(2)设cn= ![]() ,数列{cn}的前n项和为Tn .
,数列{cn}的前n项和为Tn .
①求Tn;
②对于任意的n∈N*及x∈R,不等式kx2﹣6kx+k+7+3Tn>0恒成立,求实数k的取值范围.
【答案】
(1)解:∵4Sn=(2n﹣1)an+1+1,
∴4Sn﹣1=(2n﹣3)an+1,n≥2
∴4an=(2n﹣1)an+1﹣(2n﹣3)an,
整理得(2n+1)an=(2n﹣1)an+1,
即 ![]() =
= ![]() ,
,
∴ ![]() =3,
=3, ![]() =
= ![]() ,…,
,…, ![]() =
= ![]()
以上各式相乘得 ![]() =2n﹣1,又a1=1,
=2n﹣1,又a1=1,
所以an=2n﹣1,
(2)解:①∵cn= ![]() =
= ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),
),
∴Tn= ![]() (1﹣
(1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() )=
)= ![]() (1﹣
(1﹣ ![]() )=
)= ![]() ,
,
②由①可知Tn= ![]() ,
,
∴ ![]() ≥
≥ ![]() ,
,
∵kx2﹣6kx+k+7+3Tn>0恒成立,
∴kx2﹣6kx+k+8>0恒成立,
当k=0时,8>0恒成立,
当k≠0时,则得 ![]() ,解得0<k<1,
,解得0<k<1,
综上所述实数k的取值范围为[0,1)
【解析】(1)充分利用已知4Sn=(2n﹣1)an+1+1,将式子中n换成n﹣1,然后相减得到an与an+1的关系,利用累乘法得到数列的通项,(2)①利用裂项求和,即可求出Tn ,
②根据函数的思想求出 ![]() ≥
≥ ![]() ,问题转化为kx2﹣6kx+k+8>0恒成立,分类讨论即可.
,问题转化为kx2﹣6kx+k+8>0恒成立,分类讨论即可.
【考点精析】通过灵活运用数列的前n项和和数列的通项公式,掌握数列{an}的前n项和sn与通项an的关系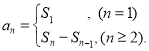 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是89.
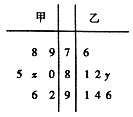
(1)求![]() 和
和![]() 的值;
的值;
(2)计算乙班7位学生成绩的方差![]() .
.
(3)从成绩在90分以上的学生中随机抽取两名学生,求乙班至少有一名学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,两焦点分别为
,两焦点分别为![]() ,右顶点为
,右顶点为![]() ,
, ![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设过定点![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 的左支有两个交点,与椭圆
的左支有两个交点,与椭圆![]() 交于
交于![]() 两点,与圆
两点,与圆![]() 交于
交于![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,
, ![]() ,求正数
,求正数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 是两条不同直线,
是两条不同直线, ![]() ,
, ![]() 是两个不同平面,则下列命题正确的是( )
是两个不同平面,则下列命题正确的是( )
A. 若![]() ,
, ![]() 垂直于同一平面,则
垂直于同一平面,则![]() 与
与![]() 平行
平行
B. 若![]() ,
, ![]() 平行于同一平面,则
平行于同一平面,则![]() 与
与![]() 平行
平行
C. 若![]() ,
, ![]() 不平行,则在
不平行,则在![]() 内不存在与
内不存在与![]() 平行的直线
平行的直线
D. 若![]() ,
, ![]() 不平行,则
不平行,则![]() 与
与![]() 不可能垂直于同一平面
不可能垂直于同一平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C为△ABC的三个内角,且其对边分别为a、b、c,若cosBcosC﹣sinBsinC= ![]() .
.
(1)求角A;
(2)若a=2 ![]() ,b+c=4,求△ABC的面积.
,b+c=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线: ![]() (
(![]() 为给定的正常数,
为给定的正常数, ![]() 为参数,
为参数, ![]() )构成的集合为
)构成的集合为![]() ,给出下列命题:
,给出下列命题:
①当![]() 时,
时, ![]() 中直线的斜率为
中直线的斜率为![]() ;
;
②![]() 中的所有直线可覆盖整个坐标平面.
中的所有直线可覆盖整个坐标平面.
③当![]() 时,存在某个定点,该定点到
时,存在某个定点,该定点到![]() 中的所有直线的距离均相等;
中的所有直线的距离均相等;
④当![]() 时,
时, ![]() 中的两条平行直线间的距离的最小值为
中的两条平行直线间的距离的最小值为![]() ;
;
其中正确的是__________(写出所有正确命题的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 点在底面
点在底面![]() 内的射影
内的射影![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 在线段
在线段![]() 上,且
上,且![]() .
.
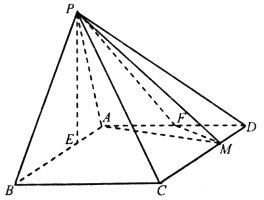
(Ⅰ)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)当平面![]() 与平面
与平面![]() 所成的二面角的正弦值为
所成的二面角的正弦值为![]() 时,求四棱锥
时,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com