
| 9 |
| sin2x |
x-
| ||
x-
|
| 1 |
| x-1 |
| 9 |
| sin2x |
| 9 |
| 9 |
| sin2x |
x-
| ||
x-
|
| ||||
(x-
|
| 10 |
| 10 |
| 1 |
| x-1 |


科目:高中数学 来源: 题型:
| π |
| 4 |
| 1 |
| 2a |
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:江西省南昌市2008-2009学年度高三调研考试模拟训练理科数学 题型:022
有以下五个命题:①若随机变量ξ服从正态分布ξ~N(3,2),η=![]() ,则随机变量η的期望是0;
,则随机变量η的期望是0;
②已知f(x)=![]() ,则f(4)>f(3);
,则f(4)>f(3);
③y=loga(2+ax)(a>0,a≠1)在R上是增函数;
④定义在R上的偶函数f(x)满足f(x+1)=f(x),则f(2)=f(0);
⑤若f(x)是定义在R上的奇函数,且f(x+2)也为奇函数,则f(x)是以4为周期的周期函数.
其中假命题的序号是________(把你认为正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州二中高三(上)10月月考数学试卷(文科)(解析版) 题型:填空题
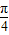 ],则点P到曲线y=f(x)对称轴距离的取值范围为[0,
],则点P到曲线y=f(x)对称轴距离的取值范围为[0, ];
]; ,那么速度为零的时刻只有1秒末;
,那么速度为零的时刻只有1秒末; 内单调递增,则a的取值范围是
内单调递增,则a的取值范围是 ;
;查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省宜春市上高二中高三(上)第一次月考数学试卷(理科)(解析版) 题型:填空题
 的最小值是6.②已知
的最小值是6.②已知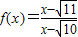 ,则f(4)<f(3).③函数f(x)值域为(-∞,0],等价于f(x)≤0恒成立.④函数
,则f(4)<f(3).③函数f(x)值域为(-∞,0],等价于f(x)≤0恒成立.④函数 在定义域上单调递减.⑤若函数y=f(x)的值域是[1,3],则函数F(x)=1-f(x+3)的值域是[-5,-3].其中真命题是: .
在定义域上单调递减.⑤若函数y=f(x)的值域是[1,3],则函数F(x)=1-f(x+3)的值域是[-5,-3].其中真命题是: .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com