
【题目】已知函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)若曲线![]() 与直线
与直线![]() 有且只有一个公共点
有且只有一个公共点![]() ,求证:
,求证:![]() .(参考数据:
.(参考数据:![]() )
)
【答案】(1)单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)对函数![]() 求导,即可得函数
求导,即可得函数![]() 的单调区间;
的单调区间;
(2)构造函数![]() ,将问题转化为函数
,将问题转化为函数![]() 有且只有一个零点
有且只有一个零点![]() ,利用导数研究函数的单调性,得到关于
,利用导数研究函数的单调性,得到关于![]() 的等式,最后构造函数,利用函数的单调性求
的等式,最后构造函数,利用函数的单调性求![]() 的取值范围,从而得证.
的取值范围,从而得证.
(1)由题意,函数![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,即
单调递增,即![]() 在
在![]() 上单调递增,
上单调递增,
因为![]() ,所以当
,所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
(2)设函数![]() ,
,
由曲线![]() 与直线
与直线![]() 有且只有一个公共点
有且只有一个公共点![]() ,
,
等价于函数![]() 有且只有一个零点
有且只有一个零点![]() ,
,
又由![]() ,
,
设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,即
单调递增,即![]() 在
在![]() 上单调递增,
上单调递增,
因为![]() ,所以存在
,所以存在![]() ,使
,使![]() ,
,
所以当![]() 时,
时,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() 单调递增,
单调递增,
而![]() ,
,
所以要使函数![]() 有且只有一个零点
有且只有一个零点![]() ,则
,则![]() ,
,
所以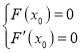 ,即
,即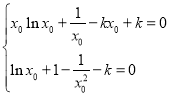 ,
,
消元得![]() .
.
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 单调递减,
单调递减,
又由![]() ,所以存在
,所以存在![]() ,使得
,使得![]() ,
,
即若曲线![]() 与直线
与直线![]() 有且只有一个公共点
有且只有一个公共点![]() ,则
,则![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中已知椭圆![]() ,焦点在x轴上的椭圆
,焦点在x轴上的椭圆![]() 与
与![]() 的离心率相同,且椭圆
的离心率相同,且椭圆![]() 的外切矩形ABCD(两组对边分别平行于x轴、y轴)的顶点在椭圆
的外切矩形ABCD(两组对边分别平行于x轴、y轴)的顶点在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)设![]() 为椭圆
为椭圆![]() 上一点(不与点A、B、C、D重合).
上一点(不与点A、B、C、D重合).
①若直线:![]() ,求证:直线l与椭圆
,求证:直线l与椭圆![]() 相交;
相交;
②记①中的直线l与椭圆C1的交点为S、T,求证![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,过点
,过点![]() 作椭圆C的切线l,在第一象限的切点为P,过点P作与直线l倾斜角互补的直线,恰好经过椭圆C的下顶点N.
作椭圆C的切线l,在第一象限的切点为P,过点P作与直线l倾斜角互补的直线,恰好经过椭圆C的下顶点N.
(1)求椭圆C的方程;
(2)F为椭圆C的右焦点,过点F且与x轴不垂直的直线![]() 交椭圆C于A,B两点,点A关于x轴的对称点为
交椭圆C于A,B两点,点A关于x轴的对称点为![]() ,则直线
,则直线![]() 是否过定点,若是,求出定点坐标;若不是,请说明理由.
是否过定点,若是,求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,椭圆![]() 的离心率为
的离心率为![]() ,过点
,过点![]() 作直线
作直线![]() 交椭圆于不同两点
交椭圆于不同两点![]() ,
,![]() .
.
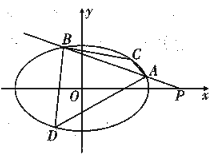
(1)求椭园的方程;
(2)①设直线的斜率为![]() ,求出与直线
,求出与直线![]() 平行且与椭圆相切的直线方程(用
平行且与椭圆相切的直线方程(用![]() 表示);
表示);
②若![]() ,
,![]() 为椭圆上的动点,求四边形
为椭圆上的动点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
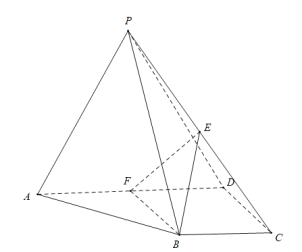
【题目】如图,在三棱台![]() 中,
中,![]() ,.若点
,.若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 靠近点
靠近点![]() 的四等分点.
的四等分点.
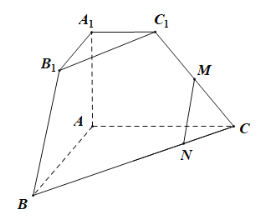
(1)求证:![]() 平面
平面![]() ;
;
(2)若三棱台![]() 的体积为
的体积为![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
注:台体体积公式:![]() ,或在
,或在![]() 分别为台体上下底面积,
分别为台体上下底面积,![]() 为台体的高.
为台体的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】回文数指从左向右读与从右向左读都一样的正整数,如22,343,1221,94249等.显然两位回文数有9个,即11,22,33,99;三位回文数有90个,即101,121,131,…,191,202,…,999.则四位回文数有______个,![]() 位回文数有______个.
位回文数有______个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,平面
的中点,平面![]() 平面
平面![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 平面
平面![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 与底面
与底面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且在[0,+∞)上单调递减,f(2)=0,则不等式f(log2x)>0的解集为( )
A.(![]() ,4)B.(2,2)C.(
,4)B.(2,2)C.(![]() ,+∞)D.(4,+∞)
,+∞)D.(4,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016高考新课标II,理15)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com