练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图2-2-8,在等腰三角形ABC中,AB =AC,D是AC中点,DE平分∠ADB,交AB于E,过A、D、E的圆交BD于N.求证:BN =2AE.

    图2-2-8

    思路分析:要证BN =2AE,由已知有AB=AC =2AD,所以只需证=.而又因为AE =NE,所以只需证=,这可由△BNE∽△BAD证得.

    证明:连结EN,∵四边形AEND是圆内接四边形,?

    ∴∠BNE =∠A.?

    又∵∠ABD =∠EBN,∴△BNE∽△BAD.?

    ∴=.?

    ∵AB =AC,AC =2AD,∴AB =2AD.?

    ∴BN =2EN.?

    又∵∠ADE =∠NDE,∴AE =EN,?

    ∴AE =EN,∴BN =2AE.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，AB∥DC，△PAD是等边三角形，已知AD=4，BD=4
    		3
    ，AB=2CD=8．
    （1）设M是PC上的一点，证明：平面MBD⊥平面PAD；
    （2）当M点位于线段PC什么位置时，PA∥平面MBD？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

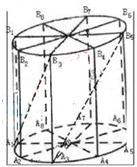    精英家教网如图所示，为了制作一个圆柱形灯笼，先要制作4个全等的矩形骨架，总计耗用9.6米铁丝，骨架把圆柱底面8等份，再用S平方米塑料片制成圆柱的侧面和下底面（不安装上底面）．
    （1）当圆柱底面半径r取何值时，S取得最大值？并求出该最大值（结果精确到0.01平方米）；
    （2）在灯笼内，以矩形骨架的顶点为点，安装一些霓虹灯，当灯笼的底面半径为0.3米时，求图中两根直线A1B3与A3B5所在异面直线所成角的大小（结果用反三角函数表示）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    有一海湾，海岸线为近似半个椭圆（如图），椭圆长轴端点为A，B，AB间距离为3km，椭圆焦点为C，D，CD间距离为2km，在C，D处分别有甲，乙两个油井，现准备在海岸线上建一度假村P，不考虑风向等因素影响，油井对度假村废气污染程度与排出废气的浓度成正比（比例系数都为k1），与距离的平方成反比（比例系数都为k2），又知甲油井排出的废气浓度是乙的8倍．
    （1）设乙油井排出的浓度为a（a为常数）度假村P距离甲油井xkm，度假村P受到甲乙两油井的污染程度和记为f（x），求f（x）的表达式并求定义域；
    （2）度假村P距离甲油井多少时，甲乙两油井对度假村的废气污染程度和最小？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•江苏二模）如图，边长为2的正方形内有一个半径为1的半圆．向正方形内任投一点（假设该点落在正方形内的每一点都是等可能的），则该点落在半圆内的概率为
    π
    8
    π
    8
    ．

    查看答案和解析>>

    科目：高中数学 来源：2013届新课标高三配套第四次月考文科数学试卷（解析版） 题型：解答题

    如图6所示，等边三角形OAB的边长为8，且其三个顶点均在抛物线E：x2＝2py(p＞0)上.

    图6

    （1）求抛物线E的方程；

    （2）设动直线l与抛物线E相切于点P，与直线y＝－1相交于点Q，证明以PQ为直径的圆恒过y轴上某定点.

     

    查看答案和解析>>

    同步练习册答案