
【题目】在直角坐标系xOy中,记函数![]() 的图象为曲线C1,函数
的图象为曲线C1,函数![]() 的图象为曲线C2.
的图象为曲线C2.
(Ⅰ)比较f(2)和1的大小,并说明理由;
(Ⅱ)当曲线C1在直线y=1的下方时,求x的取值范围;
(Ⅲ)证明:曲线C1和C2没有交点.
【答案】(Ⅰ)f(2)>1,理由见解析;(Ⅱ)(log25,3);(Ⅲ)证明见解析
【解析】
(Ⅰ)因为![]() ,求出f (2)的值,结合函数的单调性判断f (2)和1的大小.
,求出f (2)的值,结合函数的单调性判断f (2)和1的大小.
(Ⅱ)因为“曲线C在直线y=1的下方”等价于“f (x)<1”,推出![]() .求解即可.
.求解即可.
(Ⅲ)求出两个函数的定义域,然后判断曲线C1和C2没有交点.
解: (Ⅰ)因为![]() ,
,
又函数y=log3x是 (0,+∞)上的增函数,
所以f (2)=log34>log33=1.
(Ⅱ)因为“曲线C在直线y=1的下方”等价于“f (x)<1”,
所以![]() .
.
因为 函数y=log3x是 (0,+∞)上的增函数,
所以 0<8﹣2x<3,
即 5<2x<8,
所以x的取值范围是 (log25,3).
(Ⅲ)因为f (x)有意义当且仅当8﹣2x>0,
解得x<3.
所以f (x)的定义域为D1= (﹣∞,3).
g (x)有意义当且仅当x﹣3≥0,
解得x≥3.
所以g (x)的定义域为D2=[3,+∞).
因为D1∩D2=,
所以曲线C1和C2没有交点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】复利是一种计算利息的方法.即把前一期的利息和本金加在一起算作本金,再计算下一期的利息.某同学有压岁钱1000元,存入银行,年利率为2.25%;若放入微信零钱通或
者支付宝的余额宝,年利率可达4.01%.如果将这1000元选择合适方式存满5年,可以多获利息( )元.(参考数据:![]() )
)
A. 176 B. 100 C. 77 D. 88
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() 是满足下列性质的函数
是满足下列性质的函数![]() 的全体:存在实数
的全体:存在实数![]() ,对于定义域内的任意
,对于定义域内的任意![]() ,均有
,均有![]() 成立,称数对
成立,称数对![]() 为函数
为函数![]() 的“伴随数对”.
的“伴随数对”.
(1)判断函数![]() 是否属于集合
是否属于集合![]() ,并说明理由;
,并说明理由;
(2)试证明:假设![]() 为定义在
为定义在![]() 上的函数,且
上的函数,且![]() ,若其“伴随数对”
,若其“伴随数对”![]() 满足
满足![]() ,求证:
,求证:![]() 恒成立;
恒成立;
(3)若函数![]() ,求满足条件的函数
,求满足条件的函数![]() 的所有“伴随数对”.
的所有“伴随数对”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知六棱锥P﹣ABCDEF的底面是正六边形,PA⊥平面ABC,PA=AB,则下列结论正确的是_____.(填序号)①PB⊥AD;②平面PAB⊥平面PBC;③直线BC∥平面PAE;④sin∠PDA![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近期,某公交公司与银行开展云闪付乘车支付活动,吸引了众多乘客使用这种支付方式.某线路公交车准备用20天时间开展推广活动,他们组织有关工作人员,对活动的前七天使用云闪付支付的人次数据做了初步处理,设第x天使用云闪付支付的人次为y,得到如图所示的散点图.
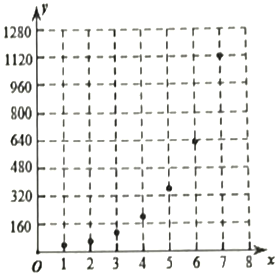
由统计图表可知,可用函数y=abx拟合y与x的关系
(1)求y关于x的回归方程;
(2)预测推广期内第几天起使用云闪付支付的人次将超过10000人次.
附:①参考数据
|
|
|
|
|
|
4 | 360 | 2.30 | 140 | 14710 | 71.40 |
表中vi=lgyi,![]() lgyi
lgyi
②参考公式:对于一组数据(u1,v1),(u2,v2)…,(un,vn),其回归直线v=α+βu的斜率和截距的最小二乘估计分别为β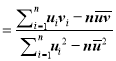 ,α
,α![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com