
【题目】已知函数![]()
![]() 的值域为
的值域为![]() ,函数
,函数![]() (
(![]() ).
).
(1)求![]() ;
;
(2)求函数![]() 的值域;
的值域;
(3)当![]() 时,若函数
时,若函数![]()
![]() 有零点,求
有零点,求![]() 的取值范围,并讨论零点的个数.
的取值范围,并讨论零点的个数.
【答案】(1)![]() (2)
(2)![]()
![]() (3)见解析
(3)见解析
【解析】
(1)利用分段函数的单调性分别求出各段的值域即可求解.
(2)设![]() ,由
,由![]() ,将函数转化为二次函数,配方即可求值域.
,将函数转化为二次函数,配方即可求值域.
(3)函数![]() 有零点,转化为函数
有零点,转化为函数![]() 与函数
与函数![]() (
(![]() )的图象有交点,由(2)可求出
)的图象有交点,由(2)可求出![]() 的取值范围;结合二次函数的图像可确定零点个数.
的取值范围;结合二次函数的图像可确定零点个数.
(1)![]() 单调递减,当
单调递减,当![]() 时,
时,![]() ,
,
![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,
,
![]() 或
或![]()
(2)设![]() ,
,![]()
![]() ,
,![]() 或
或![]() ,
,![]()
故得![]() ,
,![]()
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]()
故![]() 的值域为
的值域为![]()
![]()
因为![]() 与
与![]() 的值域相同.故
的值域相同.故![]() 的值域为
的值域为![]()
![]()
(3)函数![]() 有零点,等价于方程
有零点,等价于方程![]() 有实根,
有实根,
即方程![]() 有实根,
有实根,
因此又等价于函数![]() 与函数
与函数![]() (
(![]() )的图象有交点
)的图象有交点
由(2)知![]()
![]()
![]()
![]() ,
,
所以当且仅当![]()
![]()
![]() 时,
时,
函数![]()
![]() 有零点
有零点
下面讨论零点的个数:结合二次函数的图像与性质,由(2)可知
![]() 单调递减,
单调递减,![]() 单调递增,
单调递增,![]() 单调递增,
单调递增,
①当![]() 或当
或当![]()
![]() 时,函数只有一个零点
时,函数只有一个零点
②当![]()
![]() 时,函数有两个零点
时,函数有两个零点
③当![]()
![]() 时,函数没有零点
时,函数没有零点


科目:高中数学 来源: 题型:
【题目】已知函数g(x)=Acos(ωx+φ)+B的部分图象如图所示,将函数g(x)的图象保持纵坐标不变,横坐标向右平移![]() 个单位长度后得到函数f(x)的图象.求:
个单位长度后得到函数f(x)的图象.求:
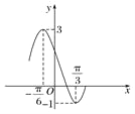
(1)函数f(x)在![]() 上的值域;
上的值域;
(2)使f(x)≥2成立的x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲同学参加化学竞赛初赛,考试分为笔试、口试、实验三个项目,各单项通过考试的概率依次为![]() 、
、![]() 、
、![]() ,笔试、口试、实验通过考试分别记4分、2分、4分,没通过的项目记0分,各项成绩互不影响.
,笔试、口试、实验通过考试分别记4分、2分、4分,没通过的项目记0分,各项成绩互不影响.
(Ⅰ)若规定总分不低于8分即可进入复赛,求甲同学进入复赛的概率;
(Ⅱ)记三个项目中通过考试的个数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知线段AB的两个端点A、B分别在x轴和y轴上滑动,且∣AB∣=2.
(1)求线段AB的中点P的轨迹C的方程;
(2)求过点M(1,2)且和轨迹C相切的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·全国卷Ⅲ文,18)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】进入春天,大气流动性变好,空气质量随之提高,自然风光越来越美,自驾游乡村游也就越来越热.某旅游景区试图探究车流量与景区接待能力的相关性,确保服务质量和游客安全,以便于确定是否对进入景区车辆实施限行.为此,该景区采集到过去一周内某时段车流量与接待能力指数的数据如表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
车流量(x千辆) | 10 | 9 | 9.5 | 10.5 | 11 | 8 | 8.5 |
接待能力指数y | 78 | 76 | 77 | 79 | 80 | 73 | 75 |
(I)根据表中周一到周五的数据,求y关于x的线性回归方程.
(Ⅱ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2,则认为该线性回归方程是可靠的.请根据周六和周日数据,判定所得的线性回归方程是否可靠?
附参考公式及参考数据:线性回归方程![]() ,其中
,其中 ;
;![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某中学甲、乙两班各随机抽取![]() 名同学,测量他们的身高(单位:
名同学,测量他们的身高(单位:![]() ),所得数据用茎叶图表示如下,由此可估计甲、乙两班同学的身高情况,则下列结论正确的是( )
),所得数据用茎叶图表示如下,由此可估计甲、乙两班同学的身高情况,则下列结论正确的是( )

A. 甲班同学身高的方差较大 B. 甲班同学身高的平均值较大
C. 甲班同学身高的中位数较大 D. 甲班同学身高在![]() 以上的人数较多
以上的人数较多
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com