
【题目】为了选拔学生参加全市中学生物理竞赛,学校先从高三年级选取60名同学进行竞赛预选赛,将参加预选赛的学生成绩(单位:分)按范围![]() ,
,![]() ,
,![]() ,
,![]() 分组,得到的频率分布直方图如图:
分组,得到的频率分布直方图如图:

(1)计算这次预选赛的平均成绩(同一组中的数据用该组区间的中点值作代表);
(2)若对得分在前![]() 的学生进行校内奖励,估计获奖分数线;
的学生进行校内奖励,估计获奖分数线;
(3)若这60名学生中男女生比例为![]() ,成绩不低于60分评估为“成绩良好”,否则评估为“成绩一般”,试完成下面
,成绩不低于60分评估为“成绩良好”,否则评估为“成绩一般”,试完成下面![]() 列联表,是否有
列联表,是否有![]() 的把握认为“成绩良好”与“性别”有关?
的把握认为“成绩良好”与“性别”有关?
成绩良好 | 成绩一般 | 合计 | |
男生 | |||
女生 | |||
合计 |
附:![]() ,
,![]()
临界值表:
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
【答案】(1)56分;(2)67.5分;(3)有![]() 的把握认为“成绩良好”与“性别”有关.
的把握认为“成绩良好”与“性别”有关.
【解析】
(1)平均值等于每组的中间值乘以该组频率再求和,即可得出结果;
(2)根据题意先求出获奖分数线所在的区间,设获奖分数线为![]() ,再由题意列出方程,即可求出结果;
,再由题意列出方程,即可求出结果;
(3)先求出成绩落在区间![]() 的人数,根据60名学生中男女生比例为
的人数,根据60名学生中男女生比例为![]() ,求出男女生人数,即可完善列联表,再由公式求出
,求出男女生人数,即可完善列联表,再由公式求出![]() ,结合临界值表即可得出结果.
,结合临界值表即可得出结果.
解:(1)预选赛的平均成绩为![]() (分).
(分).
(2)因为成绩落在区间![]() 的频率是
的频率是![]() ,成绩落在区间
,成绩落在区间![]() 的频率是
的频率是![]() ,
,![]() ,
,
所以获奖分数线落在区间![]() .
.
设获奖分数线为![]() ,则
,则![]() ,
,
解得![]() ,
,
即获奖分数线为67.5分.
(3)成绩落在区间![]() 的人数为
的人数为![]() ,
,
又60人中男女生比例为![]() ,故男生40人,女生20人,
,故男生40人,女生20人,
可得列联表如下:
成绩良好 | 成绩一般 | 合计 | |
男生 | 15 | 25 | 40 |
女生 | 3 | 17 | 20 |
合计 | 18 | 42 | 60 |
所以![]() .
.
又因为![]() ,
,
所以有![]() 的把握认为“成绩良好”与“性别”有关.
的把握认为“成绩良好”与“性别”有关.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】下列命题正确的是
(1)命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;
”;
(2)l为直线,![]() ,
,![]() 为两个不同的平面,若
为两个不同的平面,若![]() ,
,![]() ,则
,则![]() ;
;
(3)给定命题p,q,若“![]() 为真命题”,则
为真命题”,则![]() 是假命题;
是假命题;
(4)“![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
A. (1)(4)B. (2)(3)C. (3)(4)D. (1)(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】卵形线是常见曲线的一种,分笛卡尔卵形线和卡西尼卵形线,卡西尼卵形线是平面内与两个定点(叫焦点)的距离之积等于常数的点的轨迹.某同学类比椭圆与双曲线对卡西尼卵形线进行了相关性质的探究,设F1(﹣c,0),F2(c,0)是平面内的两个定点,|PF1||PF2|=a2(a是常数).得出卡西尼卵形线的相关结论:①该曲线既是轴对称图形也是中心对称图形;②若a=c,则曲线过原点;③若0<a<c,其轨迹为线段.其中正确命题的序号是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式![]() 表示的平面区别为
表示的平面区别为![]() .区域
.区域![]() 内的动点
内的动点![]() 到直线
到直线![]() 和直线
和直线![]() 的距离之积为2.记点
的距离之积为2.记点![]() 的轨迹为曲线
的轨迹为曲线![]() .过点
.过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求曲线![]() 的方程;
的方程;
(2)若![]() 垂直于
垂直于![]() 轴,
轴,![]() 为曲线
为曲线![]() 上一点,求
上一点,求![]() 的取值范围;
的取值范围;
(3)若以线段![]() 为直径的圆与
为直径的圆与![]() 轴相切,求直线
轴相切,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,前
为等差数列,前![]() 项和为
项和为![]() ,
,![]() 是首项为
是首项为![]() 的等比数列,且公比大于
的等比数列,且公比大于![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求![]() 和
和![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() ,
,![]() 为数列
为数列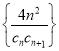 的前
的前![]() 项和,求不超过
项和,求不超过![]() 的最大整数.
的最大整数.
查看答案和解析>>
科目:高中数学 来源: 题型:
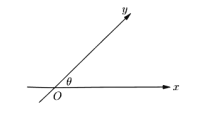
【题目】如图,数轴x、y的交点为O,夹角为![]() ,与x轴、y轴正向同向的单位向量分别是
,与x轴、y轴正向同向的单位向量分别是![]() ,
,![]() ,由平面向量基本定理,对于平面内的任一向量,存在唯一的有序实数对
,由平面向量基本定理,对于平面内的任一向量,存在唯一的有序实数对![]() ,使得
,使得![]() ,我们把
,我们把![]() 叫做点P在斜坐标系xOy中的坐标(以下各点的坐标都指在斜坐标系xOy中的坐标)
叫做点P在斜坐标系xOy中的坐标(以下各点的坐标都指在斜坐标系xOy中的坐标)
(1)若![]() ,
,![]() 为单位向量,且
为单位向量,且![]() 与
与![]() 的夹角为120°,求点P的坐标;
的夹角为120°,求点P的坐标;
(2)若![]() ,点P的坐标为
,点P的坐标为![]() ,求向量
,求向量![]() 与
与![]() 的夹角;
的夹角;
(3)若![]() ,直线l经过点
,直线l经过点![]() ,求原点O到直线l的距离的最大值.
,求原点O到直线l的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
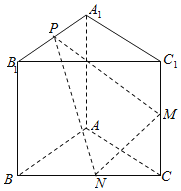
【题目】如图,已知三棱柱![]() 的侧棱与底面垂直,
的侧棱与底面垂直,![]() ,
,![]() ,M是
,M是![]() 的中点,
的中点,![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 上,且满足
上,且满足![]() .
.
(1)证明:![]() .
.
(2)当![]() 取何值时,直线
取何值时,直线![]() 与平面
与平面![]() 所成的角
所成的角![]() 最大?并求该角最大值的正切值.
最大?并求该角最大值的正切值.
(3)若平面![]() 与平面
与平面![]() 所成的二面角为
所成的二面角为![]() ,试确定P点的位置.
,试确定P点的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中,![]() ,点A是PB的中点,现沿AD将平面PAD折起,设
,点A是PB的中点,现沿AD将平面PAD折起,设![]() .
.

(1)当![]() 为直角时,求异面直线PC与BD所成角的大小;
为直角时,求异面直线PC与BD所成角的大小;
(2)当![]() 为多少时,三棱锥
为多少时,三棱锥![]() 的体积为
的体积为![]() ?
?
(3)剪去梯形中的![]() ,留下长方形纸片
,留下长方形纸片![]() ,在BC边上任取一点E,把纸片沿AE折成直二面角,问E点取何处时,使折起后两个端点
,在BC边上任取一点E,把纸片沿AE折成直二面角,问E点取何处时,使折起后两个端点![]() 间的距离最短.
间的距离最短.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com