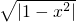练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    关于x的方程数学公式+a=x有两个不相等的实数根，试求实数a的取值范围．

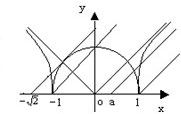    解：原方程的解可以视为函数y=x-a（y≥0）与函数y=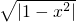的图象的交点的横坐标．
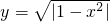    而函数的图象是由半圆y2=1-x2（y≥0）和等轴双曲线x2-y2=1（y≥0）在x轴的上半部分的图象构成．
    如图所示，当0＜a＜1或a=-，a=-1时，
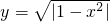    平行直线系y=x-a（y≥0）与的图象有两个不同的交点．
    所以，当0＜a＜1或a=-，a=-1时，原方程有两个不相等的实数根．
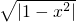    分析：原方程化为=x-a．于是，方程的解的情况可以借助于函数y=x-a（y≥0）与函数y=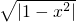的考查来进行．方程有两个不相等的实数根即两个图象有两点交点，根据图形可得实数a的取值范围．
    点评：此题要求学生掌握直线与圆的位置关系，灵活运用数形结合的数学思想解决实际问题，是一道中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若关于x的方程ax+2x-4=0（a＞0且a≠1）的所有根记作x1，x2，…，xm（m∈N*），关于x的方程loga2x+x-2=0的所有根记作x1′，x2′，…，xn′（n∈N*），则
    x1+x2+…+xm+
    x
    ′
    1
    +
    x
    ′
    2
    +…+
    x
    ′
    n
    m+n
    的值为（　　）
    A、
    1
    4
    B、
    1
    2
    C、1
    D、2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出以下四个结论：
    （1）函数f(x)=
    x-1
    x+1
    的对称中心是（-1，-1）；
    （2）若关于x的方程x-
    1
    x
    +k=0    在x∈（0，1）没有实数根，则k的取值范围是k≥2
    （3）已知点P（a，b）与点Q（1，0）在直线2x-3y+1=0两侧，则3b-2a＞1；
    （4）若将函数f(x)=sin(2x-
    π
    3
    )    的图象向右平移?（?＞0）个单位后变为偶函数，则?的最小值是
    π
    12
    其中正确的结论是：
     
    ．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年新疆农七师高级中学高二第一阶段性考试数学试卷（带解析） 题型：解答题

    ．设计一个求关于x的方程a x + b = 0的解的算法和程序框图

    查看答案和解析>>

    科目：高中数学 来源：2014届新疆农七师高级中学高二第一阶段性考试数学试卷（解析版） 题型：解答题

    ．设计一个求关于x的方程a x + b = 0的解的算法和程序框图

     

    查看答案和解析>>

    科目：高中数学 来源：2014届陕西省高一下学期期末数学试卷（解析版） 题型：解答题

    a，b，c是△ABC的三边长，关于x的方程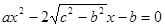 (a＞c＞b)的两根之差的平方等于4，△ABC的面积S＝10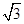，c＝7.

    (1)求角C；

    (2)求a、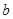的值.                                                     

     

    查看答案和解析>>

    同步练习册答案