
【题目】已知椭圆C的中心在原点,焦点在x轴上,离心率为![]() ,过椭圆C上一点P(2,1)作x轴的垂线,垂足为Q.
,过椭圆C上一点P(2,1)作x轴的垂线,垂足为Q.

(Ⅰ)求椭圆C的方程;
(Ⅱ)过点Q的直线l交椭圆C于点A,B,且3![]() +
+![]() =
=![]() ,求直线l的方程.
,求直线l的方程.
【答案】(Ⅰ)![]() ;(Ⅱ)y=±
;(Ⅱ)y=±![]() (x﹣2).
(x﹣2).
【解析】
试题分析:(Ⅰ)设椭圆![]() 的方程为
的方程为![]() ,由题意得
,由题意得![]() ,
,![]() ,解出求出
,解出求出![]() 、
、![]() 的值即可得出椭圆的方程;(Ⅱ)由题意得点
的值即可得出椭圆的方程;(Ⅱ)由题意得点![]() ,设直线方程为
,设直线方程为![]() ,将直线
,将直线![]() ,代入椭圆方程得到
,代入椭圆方程得到![]() ,利用向量的坐标运算性质、一元二次方程的根与系数的关系列方程即可得出
,利用向量的坐标运算性质、一元二次方程的根与系数的关系列方程即可得出![]() 的值,从而可求得直线方程.
的值,从而可求得直线方程.
试题解析:(Ⅰ)设椭圆C的方程为![]() +
+![]() =1(a>b>0),
=1(a>b>0),
由题意得![]() =
=![]() ,
,![]() +
+![]() =1,a2=b2+c2.
=1,a2=b2+c2.
解得a2=6,b2=c2=3,则椭圆C:![]() =
=![]() =1.
=1.
(Ⅱ)由题意得点Q(2,0),
设直线方程为x=ty+2(t≠0),A(x1,y1),B(x2,y2),
则![]() =(x1﹣2,y1),
=(x1﹣2,y1),![]() =(x2﹣2,y2),
=(x2﹣2,y2),
由3![]() +
+![]() =
=![]() ,得3y1+y2=0,
,得3y1+y2=0,
y1+y2=﹣2y1,y1y2=﹣3![]() ,得到
,得到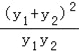 =﹣
=﹣![]() (*)
(*)
将直线x=ty+2(t≠0),代入椭圆方程得到(2+t2)y2+4ty﹣2=0,
∴y1+y2=![]() ,y1y2=
,y1y2=![]() ,代入(*)式,解得:t2=
,代入(*)式,解得:t2=![]() ,
,
∴直线l的方程为:y=±![]() (x﹣2).
(x﹣2).
【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系和平面向量的线性运算,属于难题.用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在![]() 轴上,还是在
轴上,还是在![]() 轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程
轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程![]() 或
或![]()
![]() ;③找关系:根据已知条件,建立关于
;③找关系:根据已知条件,建立关于![]() 、
、![]() 、
、![]() 的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
的方程组;④得方程:解方程组,将解代入所设方程,即为所求.


 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
【题目】供电部门对某社区![]() 位居民2017年12月份人均用电情况进行统计后,按人均用电量分为
位居民2017年12月份人均用电情况进行统计后,按人均用电量分为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五组,整理得到如下的频率分布直方图,则下列说法错误的是
五组,整理得到如下的频率分布直方图,则下列说法错误的是

A. ![]() 月份人均用电量人数最多的一组有
月份人均用电量人数最多的一组有![]() 人
人
B. ![]() 月份人均用电量不低于
月份人均用电量不低于![]() 度的有
度的有![]() 人
人
C. ![]() 月份人均用电量为
月份人均用电量为![]() 度
度
D. 在这![]() 位居民中任选
位居民中任选![]() 位协助收费,选到的居民用电量在
位协助收费,选到的居民用电量在![]() 一组的概率为
一组的概率为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下四个命题,其中正确的是( )
A. 由独立性检验可知,有![]() 的把握认为物理成绩与数学成绩有关,若某人数学成绩优秀,则他有
的把握认为物理成绩与数学成绩有关,若某人数学成绩优秀,则他有![]() 的可能物理成绩优秀;
的可能物理成绩优秀;
B. 两个随机变量相关性越强,则相关系数的绝对值越接近于![]()
C. 在线性回归方程![]() 中,当变量
中,当变量![]() 每增加一个单位时,变量
每增加一个单位时,变量![]() 平均增加
平均增加![]() 个单位
个单位
D. 线性回归方程对应的直线![]() 至少经过样本数据点中的一个点
至少经过样本数据点中的一个点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共![]() 个,生产一个卫兵需
个,生产一个卫兵需![]() 分钟,生产一个骑兵需
分钟,生产一个骑兵需![]() 分钟,生产一个伞兵需
分钟,生产一个伞兵需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 小时,若生产一个卫兵可获利润
小时,若生产一个卫兵可获利润![]() 元,生产一个骑兵可获利润
元,生产一个骑兵可获利润![]() 元,生产一个伞兵可获利润
元,生产一个伞兵可获利润![]() 元.
元.
(1)用每天生产的卫兵个数![]() 与骑兵个数
与骑兵个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎么分配生产任务才能使每天的利润最大,最大利润是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)选修4﹣2:矩阵与变换
设曲线2x2+2xy+y2=1在矩阵A= ![]() (a>0)对应的变换作用下得到的曲线为x2+y2=1.
(a>0)对应的变换作用下得到的曲线为x2+y2=1.
(Ⅰ)求实数a,b的值.
(Ⅱ)求A2的逆矩阵.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在区间D上的函数f(x),若存在闭区间[a,b]D和常数c,使得对任意x1∈[a,b],都有f(x1)=c,且对任意x2∈D,当x2[a,b]时,f(x2)<c恒成立,则称函数f(x)为区间D上的“平顶型”函数.给出下列结论:
①“平顶型”函数在定义域内有最大值;
②函数f(x)=x-|x-2|为R上的“平顶型”函数;
③函数f(x)=sin x-|sin x|为R上的“平顶型”函数;
④当t≤![]() 时,函数f(x)=
时,函数f(x)= 是区间[0,+∞)上的“平顶型”函数.
是区间[0,+∞)上的“平顶型”函数.
其中正确的结论是________.(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD, ![]() .
.
(1)证明:A1C⊥平面BB1D1D; 
(2)求平面OCB1与平面BB1D1D的夹角θ的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,使用纸板可以折叠粘贴制作一个形状为正六棱柱形状的花型锁盒盖的纸盒. 
(1)求该纸盒的容积;
(2)如果有一张长为60cm,宽为40cm的矩形纸板,则利用这张纸板最多可以制作多少个这样的纸盒(纸盒必须用一张纸板制成).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com