解答:解:当0<x≤1时,有-1<x-1<0,则f(x)=f(x-1)+1=2
x-1,
当1<x≤2时,有0<x-1≤1,则f(x)=f(x-1)+1=2
x-2+1,
当2<x≤3时,有1<x-1≤2,则f(x)=f(x-1)+1=2
x-3+2,
当3<x≤4时,有2<x-1≤3,则f(x)=f(x-1)+1=2
x-4+3,
以此类推,当n<x≤n+1(其中n∈N)时,则f(x)=f(x-1)+1=2
x-n-1+n,
所以,函数f(x)=2
x的图象与直线y=x+1的交点为:(0,1)和(1,2),
由于指数函数f(x)=2
x为增函数且图象下凸,故它们只有这两个交点.
然后:
①将函数f(x)=2
x和y=x+1的图象同时向下平移一个单位,即得到函数f(x)=2
x-1和y=x的图象,
取x≤0的部分,可见它们有且仅有一个交点(0,0).
即当x≤0时,方程f(x)-x=0有且仅有一个根x=0.
②取①中函数f(x)=2
x-1和y=x图象-1<x≤0的部分,再同时向上和向右各平移一个单位,
即得f(x)=2
x-1和y=x在0<x≤1上的图象,此时它们仍然只有一个交点(1,1).
即当0<x≤1时,方程f(x)-x=0有且仅有一个根x=1.
③取②中函数f(x)=2
x-1和y=x在0<x≤1上的图象,继续按照上述步骤进行,
即得到f(x)=2
x-2+1和y=x在1<x≤2上的图象,此时它们仍然只有一个交点(2,2).
即当1<x≤2时,方程f(x)-x=0有且仅有一个根x=2.
④以此类推,函数y=f(x)与y=x在(2,3],(3,4],…,(n,n+1]上的交点依次为(3,3),(4,4),…
(n+1,n+1).
即方程f(x)-x=0在(2,3],(3,4],…(n,n+1]上的根依次为3,4,…,n+1.
综上所述方程f(x)-x=0的根按从小到大的顺序排列所得数列为:
0,1,2,3,4,…,
其通项公式为:a
n=n-1,前n项的和为 S
n=
,
∴S
10=45,
故选C.



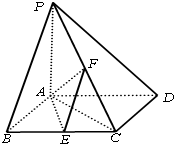 (2012•开封一模)已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
(2012•开封一模)已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.