
【题目】如图,在直四棱柱ABCD–A1B1C1D1中,已知底面ABCD是菱形,点P是侧棱C1C的中点.
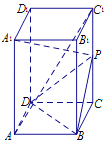
(1)求证:AC1∥平面PBD;
(2)求证:BD⊥A1P.
【答案】(1)见解析;(2)见解析
【解析】
(1)连接AC交BD于O点,连接OP,证出AC1∥OP,再由线面平行的判定定理即可证出.
(2)首先由线面垂直的判定定理证出BD⊥面AC1,再由线面垂直的定义即可证出.
(1)

连接AC交BD于O点,连接OP,
因为四边形ABCD是正方形,对角线AC交BD于点O,
所以O点是AC的中点,所以AO=OC.
又因为点P是侧棱C1C的中点,所以CP=PC1,
在△ACC1中,![]() ,所以AC1∥OP,
,所以AC1∥OP,
又因为OP面PBD,AC1面PBD,
所以AC1∥平面PBD.
(2)连接A1C1.因为ABCD–A1B1C1D1为直四棱柱,
所以侧棱C1C垂直于底面ABCD,
又BD平面ABCD,所以CC1⊥BD,
因为底面ABCD是菱形,所以AC⊥BD,
又AC∩CC1=C,AC面AC1,CC1面AC1,所以BD⊥面AC1,
又因为P∈CC1,CC1面ACC1A1,所以P∈面ACC1A1,
因为A1∈面ACC1A1,所以A1P面AC1,所以BD⊥A1P.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
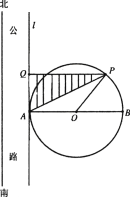
【题目】如图,在南北方向有一条公路,一半径为100![]() 的圆形广场(圆心为
的圆形广场(圆心为![]() )与此公路所在直线
)与此公路所在直线![]() 相切于点
相切于点![]() ,点
,点![]() 为北半圆弧(弧
为北半圆弧(弧![]() )上的一点,过点
)上的一点,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,计划在
,计划在![]() 内(图中阴影部分)进行绿化,设
内(图中阴影部分)进行绿化,设![]() 的面积为
的面积为![]() (单位:
(单位:![]() ),
),
(1)设![]() ,将
,将![]() 表示为
表示为![]() 的函数;
的函数;
(2)确定点![]() 的位置,使绿化面积最大,并求出最大面积.
的位置,使绿化面积最大,并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为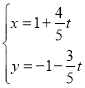 (t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=cosθ﹣sinθ.
(t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=cosθ﹣sinθ.
(1)求直线l被曲线C所截得的弦长;
(2)若M(x,y)是曲线C上的动点,求x+y的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天干地支纪年法,源于中国,中国自古便有十天干与十二地支.十天干:甲、乙、丙、丁、戊、己、庚、辛、壬、癸.十二地支:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,比如第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”,…,以此类推,排列到“癸酉”后,天干回到“甲”重新开始,即“甲戌”,“乙亥”,之后地支回到“子”重新开始,即“丙子”,…,以此类推,已知2016年为丙申年,那么到改革开放100年时,即2078年为________年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (a>0,b>0)的左右焦点分别为F1,F2,与y轴正半轴交于点B,若△BF1F2为等腰直角三角形,且直线BF1被圆x2+y2=b2所截得的弦长为2,
(a>0,b>0)的左右焦点分别为F1,F2,与y轴正半轴交于点B,若△BF1F2为等腰直角三角形,且直线BF1被圆x2+y2=b2所截得的弦长为2,
(1)求椭圆的方程;
(2)直线l:y=kx+m与椭圆交于点A,C,线段AC的中点为M,射线MO与椭圆交于点P,点O为△PAC的重心,求证:△PAC的面积S为定值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1),在平面五边形![]() 中,已知四边形
中,已知四边形![]() 为正方形,
为正方形,![]() 为正三角形.沿着
为正三角形.沿着![]() 将四边形
将四边形![]() 折起得到四棱锥
折起得到四棱锥![]() ,使得平面
,使得平面![]() 平面
平面![]() ,设
,设![]() 在线段
在线段![]() 上且满足
上且满足![]() ,
,![]() 在线段
在线段![]() 上且满足
上且满足![]() ,
,![]() 为
为![]() 的重心,如图(2).
的重心,如图(2).
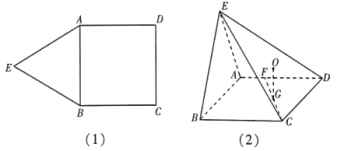
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市的公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间![]() 与乘客等候人数
与乘客等候人数![]() 之间的关系,经过调查得到如下数据:
之间的关系,经过调查得到如下数据:
间隔时间/分 | 10 | 11 | 12 | 13 | 14 | 15 |
等候人数y/人 | 23 | 25 | 26 | 29 | 28 | 31 |
调查小组先从这![]() 组数据中选取
组数据中选取![]() 组数据求线性回归方程,再用剩下的
组数据求线性回归方程,再用剩下的![]() 组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数
组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数
与实际等候人数![]() 的差,若差值的绝对值都不超过
的差,若差值的绝对值都不超过![]() ,则称所求方程是“恰当回归方程”.
,则称所求方程是“恰当回归方程”.
(1)从这![]() 组数据中随机选取
组数据中随机选取![]() 组数据后,求剩下的
组数据后,求剩下的![]() 组数据的间隔时间不相邻的概率;
组数据的间隔时间不相邻的概率;
(2)若选取的是后面![]() 组数据,求
组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判断此方程是否是“恰当回归方程”;
,并判断此方程是否是“恰当回归方程”;
(3)为了使等候的乘客不超过![]() 人,试用(2)中方程估计间隔时间最多可以设置为多少(精确到整数)分钟.
人,试用(2)中方程估计间隔时间最多可以设置为多少(精确到整数)分钟.
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
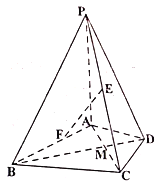
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() 是正三角形,
是正三角形,![]() 与
与![]() 的交点
的交点![]() 恰好是
恰好是![]() 中点,又
中点,又![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)设![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,若直线
上,若直线![]() 平面
平面![]() ,求
,求![]() 的长;
的长;
(3)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com