
【题目】已知中心在坐标原点,焦点在x轴上的椭圆,离心率为 ![]() 且过点(
且过点( ![]() ,0),过定点C(﹣1,0)的动直线与该椭圆相交于A、B两点.
,0),过定点C(﹣1,0)的动直线与该椭圆相交于A、B两点.
(1)若线段AB中点的横坐标是﹣ ![]() ,求直线AB的方程;
,求直线AB的方程;
(2)在x轴上是否存在点M,使 ![]() 为常数?若存在,求出点M的坐标;若不存在,请说明理由.
为常数?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】
(1)
解:由题意可设椭圆的标准方程为: ![]() =1(a>b>0),
=1(a>b>0),
∴ ![]() ,a=
,a= ![]() ,a2=b2+c2,
,a2=b2+c2,
解得a= ![]() ,c=
,c= ![]() ,b2=
,b2= ![]() .
.
∴椭圆的方程为x2+3y2=5,
直线斜率不存在时显然不成立,设直线AB:y=k(x+1),
将AB:y=k(x+1)代入椭圆的方程,消去y整理得(3k2+1)x2+6k2x+3k2﹣5=0,
设A(x1,y1),B(x2,y2),则  ,
,
∵线段AB的中点的横坐标为 ![]() ,解得
,解得 ![]() ,
,
∴直线AB的方程为 ![]()
(2)
解:假设在x轴上存在点M(m,0),使得MAMB为常数,
①当直线AB与x轴不垂直时,由(1)知 ![]() ,
,
∴ ![]() =(x1﹣m)(x2﹣m)+y1y2=(k2+1)x1x2+(k2﹣m)(x1+x2)+k2+m2=
=(x1﹣m)(x2﹣m)+y1y2=(k2+1)x1x2+(k2﹣m)(x1+x2)+k2+m2= ![]() ,
,
∵ ![]() 是与k无关的常数,从而有
是与k无关的常数,从而有 ![]() ,
,
此时 ![]() =
= ![]() .
.
②当直线AB与x轴垂直时,此时结论成立,
综上可知,在x轴上存在定点 ![]() ,使
,使 ![]() ,为常数
,为常数
【解析】(1)由题意可设椭圆的标准方程为: ![]() =1(a>b>0),可得
=1(a>b>0),可得 ![]() ,a=
,a= ![]() ,a2=b2+c2 , 解出可得椭圆的方程.直线斜率不存在时显然不成立,设直线AB:y=k(x+1),将AB:=k(x+1)代入椭圆的方程,消去y整理得(3k2+1)x2+6k2x+3k2﹣5=0,由线段AB的中点的横坐标为
,a2=b2+c2 , 解出可得椭圆的方程.直线斜率不存在时显然不成立,设直线AB:y=k(x+1),将AB:=k(x+1)代入椭圆的方程,消去y整理得(3k2+1)x2+6k2x+3k2﹣5=0,由线段AB的中点的横坐标为 ![]() ,解得k,即可得出.(2)假设在x轴上存在点M(m,0),使得MAMB为常数,
,解得k,即可得出.(2)假设在x轴上存在点M(m,0),使得MAMB为常数,
①当直线AB与x轴不垂直时,利用根与系数的关系与数量积运算性质可得 ![]() =(x1﹣m)(x2﹣m)+y1y2 , 即可得出.
=(x1﹣m)(x2﹣m)+y1y2 , 即可得出.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点在原点,焦点在x轴上,且抛物线上有一点P(4,m)到焦点的距离为6.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若抛物线C与直线y=kx﹣2相交于不同的两点A、B,且AB中点横坐标为2,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:y=2x+m与圆O:x2+y2=1相交于A,B两个不同的点,且A(cosα,sinα),B(cosβ,sinβ).
(1)当△AOB面积最大时,求m的取值,并求出|AB|的长度.
(2)判断sin(α+β)是否为定值;若是,求出定值的大小;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分16分)已知数列![]() (
(![]() ,
, ![]() )满足
)满足![]() ,
,  其中
其中![]() ,
, ![]() .
.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的表达式,并求
的表达式,并求![]() 的取值范围;
的取值范围;
(2)设集合![]() .
.
①若![]() ,
, ![]() ,求证:
,求证: ![]() ;
;
②是否存在实数![]() ,
, ![]() ,使
,使![]() ,
, ![]() ,
, ![]() 都属于
都属于![]() ?若存在,请求出实数
?若存在,请求出实数![]() ,
, ![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)如图,四棱锥![]() 的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,
的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,连结
的中点,连结![]() .求证:
.求证:
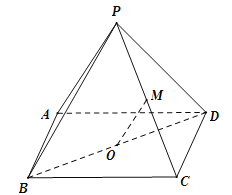
(1)![]() ∥平面
∥平面![]() ;
;
(2)![]() ⊥平面
⊥平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为12万元时,销售收入y的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足an+2SnSn﹣1=0(n≥2),a1= ![]() .
.
(1)求证:{ ![]() }是等差数列;
}是等差数列;
(2)求an的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,D为AB的中点.
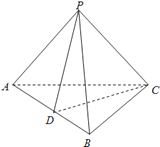
(1)与BC平行的平面PDE交AC于点E,判断点E在AC上的位置并说明理由如下:
(2)若PA=PB,且△PCD为锐角三角形,又平面PCD⊥平面ABC,求证:AB⊥PC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com