
【题目】4个不同的球,4个不同的盒子,把球全部放入盒内.
(1)恰有1个盒不放球,共有几种放法?
(2)恰有1个盒内有2个球,共有几种放法?
(3)恰有2个盒不放球,共有几种放法?
【答案】(1)144(2)144(3)84
【解析】
试题分析:(1)为保证“恰有1个盒不放球”,先从4个盒子中任意取出去一个,问题转化为“4个球,3个盒子,每个盒子都要放入球,共有几种放法?”即把4个球分成2,1,1的三组,然后再从3个盒子中选1个放2个球,其余2个球放在另外2个盒子内,由分步计数原理,共有![]() (种)
(种)
(2)“恰有1个盒内有2个球”,即另外3个盒子放2个球,每个盒子至多放1个球,也即另外3个盒子中恰有一个空盒,因此,“恰有1个盒内有2个球”与“恰有1个盒不放球”是同一件事,所以共有144种放法.
(3)确定2 个空盒有![]() 种方法.
种方法.
4个球放进2个盒子可分成![]() 两类,第一类有序不均匀分组有
两类,第一类有序不均匀分组有![]() 种方法;第二类有序均匀分组有
种方法;第二类有序均匀分组有![]() 种方法,故共有
种方法,故共有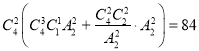 (种)放法.
(种)放法.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】通过随机询问150名大学生是否参加某社团活动,得到如下的列联表:
男 | 女 | 总计 | |
参加 | 55 | 25 | 80 |
不参加 | 30 | 40 | 70 |
总计 | 85 | 65 | 150 |
附表:
P(K2≥k0) | 0.05 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确的结论是( )
A. 在犯错的概率不超过0.1%的前提下,认为“是否参加该社团活动与性别无关”
B. 在犯错的概率不超过0.1%的前提下,认为“是否参加该社团活动与性别有关”
C. 有99%以上的把握认为“是否参加该社团活动与性别有关”
D. 有99%以上的把握认为“是否参加该社团活动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线 a . b 都在平面 外,以下假命题的是( )
A.a∥b , b∥ ,则 a∥B.a⊥b , b⊥ ,则 a∥
C.a∥ , b∥ ,则 a∥bD.a⊥ , b⊥ ,则 a∥b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某公司生产某款手机的年固定成本为40万元,每生产1万只还需另投入16万元.设该公司一年内共生产该款手机![]() 万只并全部销售完,每万只的销售收入为
万只并全部销售完,每万只的销售收入为![]() 万元,且
万元,且
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万只)的函数解析式;
(万只)的函数解析式;
(2)当年产量为多少万只时,该公司在该款手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学毕业生小王相应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店,该店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元,每月可卖出300件,市场调查反映:调整价格时,售价每涨1元每月要少卖10件;售价每下降1元每月多卖20件,为获得更大的利润,现将饰品售价调整为![]() (元/件)(
(元/件)(![]() 即售价上涨,
即售价上涨,![]() 即售价下降),每月饰品销售为
即售价下降),每月饰品销售为![]() (件),月利润为
(件),月利润为![]() (元).
(元).
(1)直接写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如何确定销售价格才能使月利润最大?求最大月利润;
(3)为了使每月利润不少于6000元,应如何控制销售价格?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知从![]() 地到
地到![]() 地共有两条路径
地共有两条路径![]() 和
和![]() ,据统计,经过两条路径所用的时间互不影响,且经过
,据统计,经过两条路径所用的时间互不影响,且经过![]() 和
和![]() 所用时间落在各时间段内的频率分布直方图分别为下图(1)和(2)。
所用时间落在各时间段内的频率分布直方图分别为下图(1)和(2)。

现甲、乙两人分别有40分钟和50分钟时间用于从![]() 地到
地到![]() 地。
地。
(1)为了尽最大可能在各自允许的时间内赶到![]() 地,甲和乙应如何选择各自的路径?
地,甲和乙应如何选择各自的路径?
(2)用![]() 表示甲、乙两人中在允许的时间内能赶到
表示甲、乙两人中在允许的时间内能赶到![]() 地的人数,针对(1)的选择方案,求
地的人数,针对(1)的选择方案,求![]() 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后抛掷两枚均匀的正方体骰子,观察向上的点数,问:
(1)共有多少种不同的结果?
(2)所得点数之和是11的概率是多少?
(3)所得点数之和是4的倍数的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com