Question

【题目】在平面直角坐标系中，直线l的方程为x+y+3=0，以直角坐标系中x轴的正半轴为极轴的极坐标系中，圆M的极坐标方程为ρ=2sinθ． （Ⅰ）写出圆M的直角坐标方程及过点P（2，0）且平行于l的直线l1的参数方程；
（Ⅱ）设l1与圆M的两个交点为A，B，求 的值．

Answer 1

【答案】解：（Ⅰ）极坐标方程ρ=2sinθ两边同乘ρ，得ρ2=2ρsinθ 其中ρ2=x2+y2 ， y=ρsinθ，x=ρcosθ
所以⊙M的直角坐标方程为x2+y2﹣2y=0…①
又直线x+y+3=0的倾斜角为 ，
所以过点P（2，0）且平行于x+y+3=0的直线的参数方程为
即 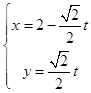，（t为参数）…②
直线的参数方程不唯一，只要正确给分
（Ⅱ）把（Ⅰ）中的②代入①整理得
设方程的两根为t1 ， t2 ， 则有
由参数t 的几何意义知PA+PB=t1+t2 ， PA*PB=t1t2
所以
【解析】（Ⅰ）极坐标方程ρ=2sinθ两边同乘ρ，得ρ2=2ρsinθ，从而能求出⊙M的直角坐标方程，直线x+y+3=0的倾斜角为 ，由此能求出过点P（2，0）且平行于x+y+3=0的直线的参数方程．（Ⅱ）把直线的参数方程代入圆的直角坐标方程，得 ，由参数t 的几何意义能求出 的值．