
函数f(x)=Asin(wx+j)(A>0,w>0,- <j<
<j< ,x∈R)的部分图象如图所示:
,x∈R)的部分图象如图所示: ,
,
(1)求函数y=f(x)的解析式;(2)当x∈ 时,求f(x)的取值范围.
时,求f(x)的取值范围.
(1)f(x)=sin(x+ );(2)[-1,
);(2)[-1, ].
].
解析试题分析:(1)图像离平衡位置最高值为1可知A=1,又从图可看出周期的四分之一为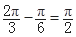 ,根据
,根据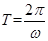 可求得w的值,对于j可通过代入(
可求得w的值,对于j可通过代入(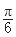 ,1)点求得,但要注意j的范围;(2)本小题考查三角函数求值域问题,由x的范围可先求出x+
,1)点求得,但要注意j的范围;(2)本小题考查三角函数求值域问题,由x的范围可先求出x+ 的范围,结合正弦函数图像可求出sin(x+
的范围,结合正弦函数图像可求出sin(x+ )的取值范围.
)的取值范围.
试题解析:(1)由图象得A=1,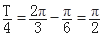 ,所以T=2p,则w="1." 将点(
,所以T=2p,则w="1." 将点(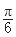 ,1)代入得sin(
,1)代入得sin(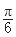 +j)=1,而-
+j)=1,而- <j<
<j< ,所以j=
,所以j= ,因此函数f(x)=sin(x+
,因此函数f(x)=sin(x+ ).
).
(2)由于x∈ ,-
,-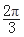 ≤x+
≤x+ ≤
≤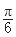 ,所以-1≤sin(x+
,所以-1≤sin(x+ )≤
)≤ ,所以f(x)的取值范围[-1,
,所以f(x)的取值范围[-1, ].
].
考点:由三角函数的图像求函数的解析式,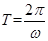 ,三角函数的值域问题.
,三角函数的值域问题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com